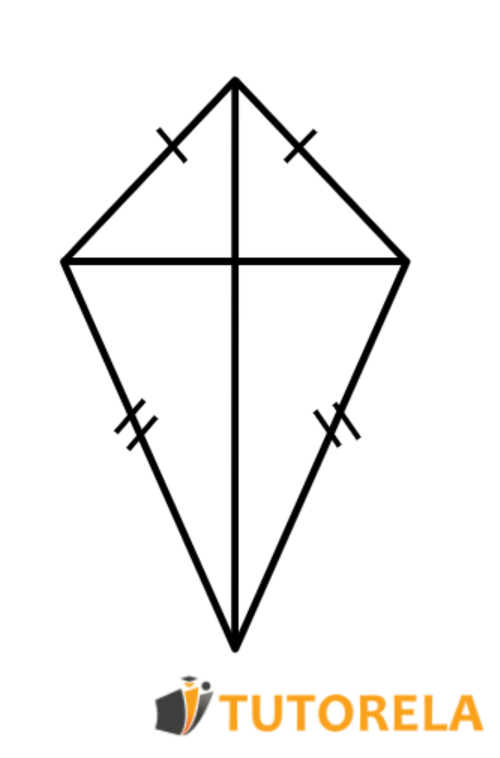
In geometry, a deltoid is defined as a quadrilateral consisting of isosceles triangles that share a common base.
So, what is the identification of a deltoid in the family of quadrilaterals?
A quadrilateral that has 2 pairs of equal adjacent sides
Example:
If given :
Then: is a deltoid by definition.
- 2 isosceles triangles with a common base form a deltoid.
- The sum of the angles in the deltoid is degrees.
- The area of the deltoid contains the number of quadrilaterals that cover the selected parts of the plane.
- The perimeter of the deltoid is the length of the thread with which we border the outline of the deltoid and is measured in units of length in meters or cm.