A cylinder must be distinguished between total surface area and lateral surface area.
Cylinder Surface Area
Calculation of the area of a cylinder
Surface area
Total surface area is the sum of the areas of the two bases and the lateral area (marked as ). The area of the base is And to obtain the area of the two bases we multiply by , that is, .
To calculate the lateral area, we return to the sliced form. The width of therectangle is While the length of the rectangle (we denote it by ) is equal to the circumference of the circle. The circumference of the circle is calculated using the formula. .
From this we get that the lateral area is the area of the sliced rectangle, and we must multiply the length of the rectangle by the width of the rectangle.
The area of the resulting rectangle is .
To obtain the total surface area, we will add the area of the two bases and the lateral area. We will eliminate a common factor outside of the parentheses. And we obtain the following formula:
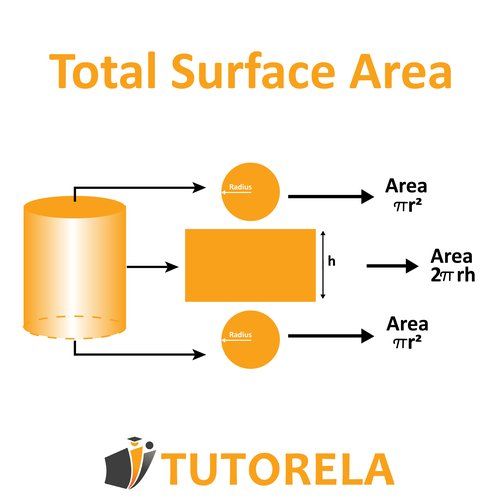
Lateral surface area
The lateral surface area is just the lateral surface, without the bases (marked as ). That is, we refer to the area of the sliced rectangle, which we have already calculated for the total surface area.
The formula is:
Examples and Practice of the Cylinder
Exercise No. 1
Given the cylinder shown in the figure.
Depending on the data, one must find the lateral surface area and the total surface area.
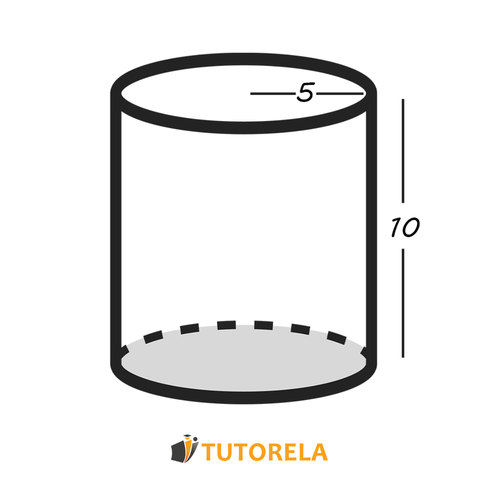
Task:
What is the total surface area of the cylinder: ?
Solution:
From the figure, it can be observed that the radius of the bases is cm, and the height of the cylinder is cm.
Now it only remains to apply the formulas we have learned.
Lateral surface area
Total surface area of the cylinder:
Answer:
The lateral surface is cm², the total surface is cm².
If you are interested in this article, you might be interested in the following articles:
The bases of the right triangular prism
The lateral faces of the prism
Surface area of triangular prisms
In the Tutorela blog, you will find a wide variety of mathematics articles
- Elements of the circumference
- Circle
- Area of a circle
- Distance from a chord to the center of a circle
- Chords of a Circle
- Central Angle in a Circle
- Arcs in a Circle
- Perpendicular to a chord from the center of a circle
- Inscribed angle in a circle
- Tangent to a circle
- The Circumference of a Circle
- How is the radius calculated using its circumference?
- Cylinder Volume
- Cuboids
- Cubes
- How to calculate the surface area of a rectangular prism (orthohedron)
- How to calculate the volume of a rectangular prism (orthohedron)
- Lateral surface area of a rectangular prism
- Right Triangular Prism
- Bases of the Right Triangular Prism
- The lateral faces of the prism
- Lateral Edges of a Prism
- Height of a Prism
- The volume of the prism
- Surface area of triangular prisms
- Circuit Components








