Chords of a Circle

A chord in a circle is a straight line that connects $2$ any points that are on the circle.
• The chord passes inside the circle and not over it.
• The longest chord in the circle is the diameter
• The radius is not a chord.

Detailed explanation

Start practice

Test yourself on the parts of a circle!

In which of the circles is the point marked in the circle and not on the circumference?

Practice more now

Chords in a Circle

We are here to explain to you what a chord in a circle is in the easiest and most logical way so that you remember it naturally.
Ask yourself... where have you encountered chords in everyday life?
Know that there are strings on a guitar.
Let's remember what they are like:

We see that the strings pass over the circle in the center of the guitar and that each string connects two points on the circle.
Now, it will be easier for us to remember and naturally understand the properties of the string in the circle.
What is a string in a circle?

A chord in a circle is a straight line that connects any 2 points that are on top of the circle.
The chord passes inside the circle.

Let's show it in the figure:

In front of us is a circle.
If we take $2$ points on the top part of the circle and pass a straight line between them that will pass inside the circle,
it will be called a chord.
Pay attention - the line must not pass through the center of the circle (diameter) and can pass between any of the two points that are on the circle.
Tip:
You can imagine the guitar's circle and remember what its strings are like.

Important Facts You Should Know

Is the diameter a chord?
Absolutely! The diameter is not just any chord, but it is the longest chord of the circle!
The diameter is a chord that passes through the center of the circle and, therefore, is the longest, connecting $2$ points with the greatest distance in the circle.

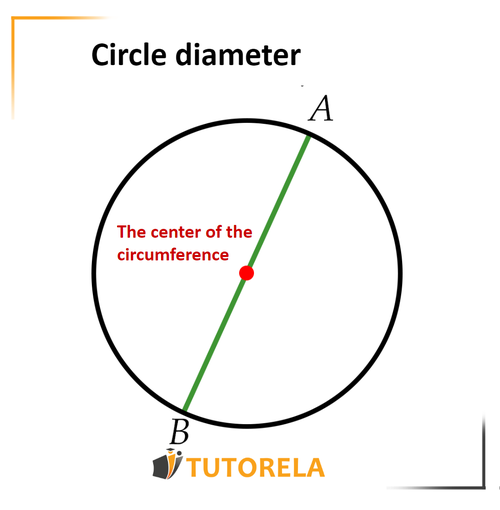
The diameter is a chord that passes through the center of the circle and, therefore, is the longest

Since the green line is a straight line connecting $2$ points on the circle, it is called a chord.

Is the radius a chord?
Absolutely not!
The definition of a chord is a straight line that passes between $2$ points located on the circle.
The radius is the line that connects the center of the circle with a point on the circle and therefore is not a chord.

Wonderful!
Now you know everything you need to know about a chord and can recognize it even in your sleep.

If you are interested in this article, you might also be interested in the following articles:

In the Tutorela blog, you will find a variety of articles about mathematics.

Examples and exercises with solutions of chords in a circle

Exercise #1

A point whose distance from the center of the circle is _______ than the radius, is outside the circle.

Step-by-Step Solution

Let's remember that the circle is actually the inner part of the circumference, meaning the enclosed area within the frame of the circumference.

Therefore, a point whose distance is greater than the center of the circle will necessarily be outside the circle.

Answer

greater

Exercise #2

Where does a point need to be so that its distance from the center of the circle is the shortest?

Step-by-Step Solution

Let's remember that the circle is actually the inner part of the circumference, meaning the enclosed area within the frame of the circumference.

Therefore, a point whose distance is less than the radius from the center of the circle will necessarily be inside the circle.

Answer

Inside

Exercise #3

In which of the circles is the segment drawn the radius?

Video Solution

Step-by-Step Solution

Let's remember that a radius is a line segment connecting the center of the circle to a point that lies on the circle itself.

In drawing A, the line doesn't touch any point on the circle itself.

In drawing B, the line doesn't pass through the center of the circle.

We can see that in drawing C, the line that extends from the center of the circle is indeed connected to a point on the circle itself.

Answer

Exercise #4

Which diagram shows the radius of a circle?

Step-by-Step Solution

Let's remember that a radius is a line segment connecting the center of a circle to any point on the circle itself.

In drawing C we can see that the line coming from the center of the circle indeed connects to a point on the circle itself, while in the other drawings the lines don't touch any point on the circle.

Therefore, C is the correct drawing.