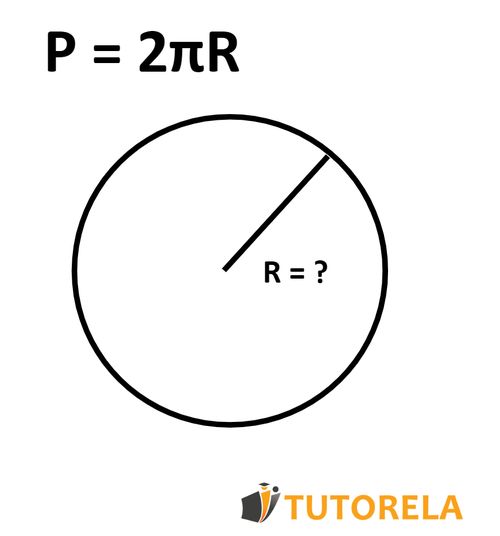
Some of you may know the radius as a "dial". Either way, the meaning is identical with the same characteristics. So, what is the radius? It is a specific segment that connects the center of a circle with a particular point on the circumference .
How is the radius calculated using its circumference?
How is the radius calculated using its perimeter?
The formula for calculating the perimeter or circumference of a circle is:
Where is the perimeter of the circle, is the radius of the circle, and is a number approximately equal to .
Given: A circle with a circumference of . The radius of the circle needs to be calculated.
We will place the known data into the formula:
The perimeter can be translated in terms of , that is:
Then we obtain:
Reduce the value of and get . Continue with a division by to isolate the value of .
That is: and, therefore, the result obtained is that the radius of the circle .
Test yourself on circumference!
O is the center of the circle in the diagram.
What is its perimeter?
Another way to solve:

More examples:
Given: A circle whose perimeter is , we must calculate the radius of the circle
We will place the data we know into the formula:
The circumference can be translated in terms of , that is:
Then we obtain:
To isolate the value of divide
Therefore, the result is that the radius of the circle
Given a circle with a circumference of , we must calculate the radius of the circle
We will place the known data into the formula:
The circumference can be expressed in terms of , that is:
Then we obtain:
To isolate the value of , it is necessary to divide
Therefore, the result is that the radius of the circle
The data of a circle whose circumference is , the radius of the circle must be calculated.
To isolate the value of divide
Therefore, the result is that the radius of the circle
\( r=7 \)
Calculate the circumference.
\( r=6 \)
Calculate the circumference.
\( r=11 \)
Calculate the circumference.
Exercises on Calculating Radius and Circumference
Exercise 1:
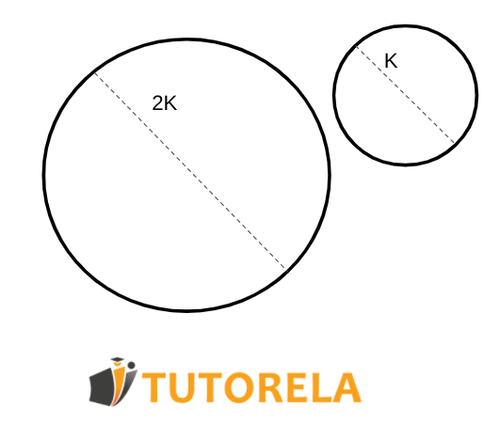
Task:
How will the circumference change if we double its diameter?
Solution:
The radius is equal to
The radius is equal to
Answer:
The circumference will double
Exercise 2:
Given the shape of the figure.
The quadrilateral is a square with cm side length.
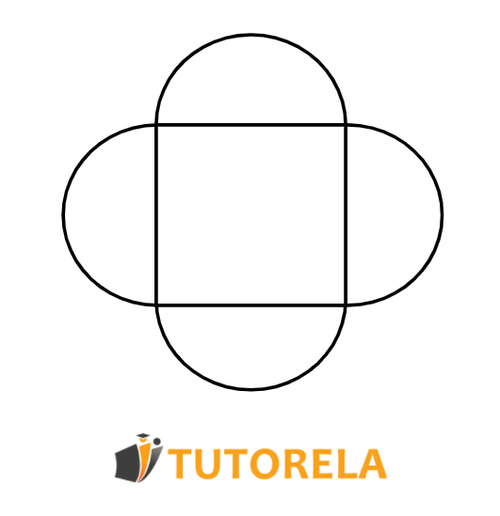
Task:
What is the perimeter of the figure?
Solution:
The perimeter is made up of halves of the circle.
That is, a total of circumferences with cm diameter.
Circle diameter cm
Answer:
Exercise 3:
Given:
Mirta runs at a speed of minutes per kilometer.
She runs on a circular path with a radius of meters and circles it times.
Task:
How long will Mirta run?
Solution:
First, we calculate the length of the path.
Path length = The circumference has a radius of meters.
Mirta's path distance = Path length = (meters)
That is: km
Answer:
It will take Mirta minutes to complete the run.
Exercise 4:
Given the circle with a circumference of

Question:
What is its area?
Solution:
Let's recall the circumference formula:
We replace with the known data:
We divide by
Now we divide by
From here we can replace the data in the area formula of the circumference:
Answer:
```
How to Calculate the Radius Using Its Circumference? (Examples and Exercises with Solutions)
Exercise #1
O is the center of the circle in the diagram.
What is its perimeter?
Video Solution
Step-by-Step Solution
To solve this problem, we will determine the circumference of the circle:
- Step 1: Identify the radius, . From the diagram, the number is provided, suggesting that cm.
- Step 2: Use the circumference formula for a circle: .
- Step 3: Substitute the radius into the formula: cm.
Therefore, the circumference of the circle is cm. This aligns with choice 3 from the provided options.
The correct and verified circumference is cm.
Answer
cm
Exercise #2
Calculate the circumference.
Video Solution
Step-by-Step Solution
To solve the problem of finding the circumference of a circle with radius , we will follow these steps:
- Step 1: Identify the given value of the radius.
- Step 2: Apply the formula for the circumference of a circle.
- Step 3: Calculate the result using known values.
Let's go through these steps in detail:
Step 1: The radius is given as .
Step 2: The formula for the circumference of a circle is .
Step 3: Substitute the given radius into the formula:
Using the value of , we can calculate:
Therefore, the circumference of the circle is approximately .
Answer
43.982
Exercise #3
Calculate the circumference.
Video Solution
Step-by-Step Solution
To solve this problem, follow these steps:
- Step 1: Given that the radius .
- Step 2: Use the formula for the circumference of a circle, .
- Step 3: Substitute the radius into the formula: .
- Step 4: Calculate the expression: .
- Step 5: Approximate to find .
- Step 6: Perform the multiplication: .
- Step 7: Round off the number to three decimal places: .
The correct answer matches the choice labeled 2: 37.699.
Answer
37.699
Exercise #4
Calculate the circumference.
Video Solution
Step-by-Step Solution
To solve this problem, we'll follow these steps:
- Step 1: Identify the given information
- Step 2: Apply the appropriate formula
- Step 3: Perform the necessary calculations
Now, let's work through each step:
Step 1: The problem provides the radius of the circle as .
Step 2: We'll use the formula for the circumference of a circle: .
Step 3: Plugging in the value of the radius, , into the formula, we get:
.
Using approximately , we calculate:
.
Therefore, the circumference of the circle is approximately 69.115.
Upon comparing this with the given choices, the correct choice is:
Choice 4:
69.115
Answer
69.115
Exercise #5
Look at the circle in the figure:
Its radius is equal to 4.
What is its circumference?
Video Solution
Step-by-Step Solution
The formula for the circumference is equal to:
Answer
8π
Take a Breather: 5 Excellent Tips for Effective Learning Before Exams
More and more students are lamenting the way they are taught the material- that they are not taught how to study for exams. There is a big difference between solving a question in class with the teacher and with the help of classmates, and dealing with questions in real time during the exam. The secret to success? Practice the material and mentally prepare to believe in yourself, and above all, reduce feelings of stress. So, how do you prepare for the exam in the best way?
1. Start studying about a week and a half before the exam
Some schools distribute the exam schedule to students on the first day of classes. This means that you know when you will be tested, so you can prepare in advance according to your own time and priorities. A week and a half is a sufficient amount of time to study for a math exam, assuming that you have mastered most of the material and need this period just for practice and memorizing formulas.
2. Create a detailed personal learning program.
Additionally, it's worth creating a schedule for yourself that details what you will study each day of the week. It's not enough to say: "On Monday, I will study circles and radii", but you should specify exactly what you are doing:
- List the hours. For example: from 4:00 PM to 8:00 PM.
- What will you do exactly (memorize formulas, review the properties of shapes, solve exercises)?
- In just a few pages, you will progress through the workbook and so on.
3. Breaks during learning are very important
When creating a learning schedule for yourself, also incorporate breaks. If you study for hours on end and intensely, you can reach burnout quickly. The goal is to maintain your motivation and not to arrive at a pre-exam situation of exhaustion. For every two hours of study, take a fresh half-hour break.
4. Learning Groups!
Is it worth studying with friends? Yes! Just make sure that you're actually studying and it's not turning into an impromptu party. Every three days of study, use a study group with 2-3 members. The goal is to solve exercises together, while each of you can contribute your knowledge to the other members and thus strengthen certain topics. Those of you who want to simulate an exam situation can open timers and check how much time it takes to solve the exercises.
5. Come to math class with questions.
During home study, it's likely that some more challenging and complex questions will arise, which is fine. Teachers allow you to raise questions that you want them to solve in class, and it's definitely worth asking questions. Your teacher will guide you through solving the question, while you will learn how to deal with questions at this specific level during the test.
And what about a private tutor? A personalized math class can definitely contribute to your understanding. The recommendation is not to wait for private lessons only just before the exam, but to make sure you gradually assimilate the material learned throughout your studies. The private lesson can be conducted at the student's home, at the teacher's home, or online.
Look at the circle in the figure below.
The radius of the circle is equal to 8.
What is its perimeter?
Look at the circle in the figure below.
The radius of the circle equals 5.
What is its perimeter?
Look at the circle in the figure.
What is its circumference given that its radius is equal to 6?
More Questions
Circumference
- Area
- Trapezoids
- Area of a trapezoid
- Perimeter of a trapezoid
- Parallelogram
- The area of a parallelogram: what is it and how is it calculated?
- Perimeter of a Parallelogram
- Elements of the circumference
- Circle
- Diameter
- Pi
- Area of a circle
- Distance from a chord to the center of a circle
- Chords of a Circle
- Central Angle in a Circle
- Arcs in a Circle
- Perpendicular to a chord from the center of a circle
- Inscribed angle in a circle
- Tangent to a circle
- The Circumference of a Circle
- The Center of a Circle
- Radius
- How is the radius calculated using its circumference?
- Rectangle
- Calculating the Area of a Rectangle
- The perimeter of the rectangle
- Perimeter
- Triangle
- The Area of a Triangle
- Area of a right triangle
- Area of Isosceles Triangles
- Area of a Scalene Triangle
- Area of Equilateral Triangles
- Perimeter of a triangle
- Cylinder Surface Area
- Cylinder Volume
- Areas of Polygons for 7th Grade
- Area of a right-angled trapezoid
- Area of an isosceles trapezoid
- How do we calculate the area of complex shapes?
- How to calculate the area of a triangle using trigonometry?
- How do we calculate the perimeter of polygons?
- Parts of a Circle
- Circuit Components









