<p>Which diagram shows the radius of a circle?</p>

Perpendicular to the chord from the center of the circle

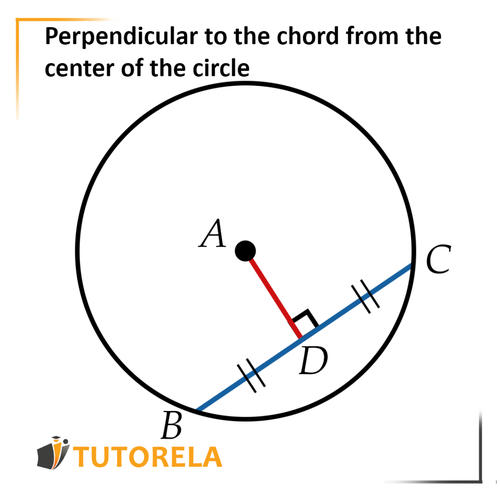
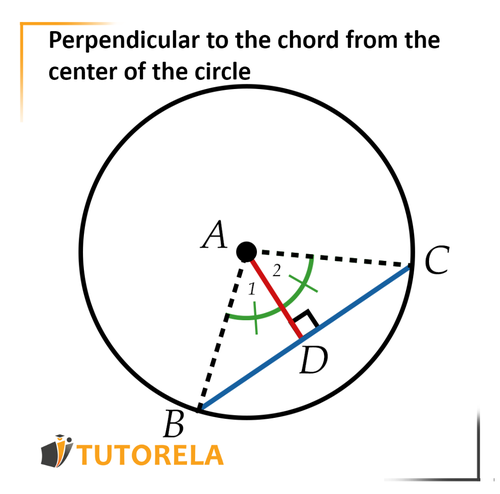
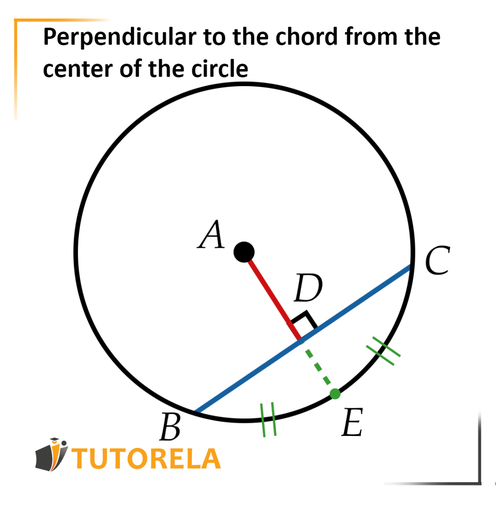
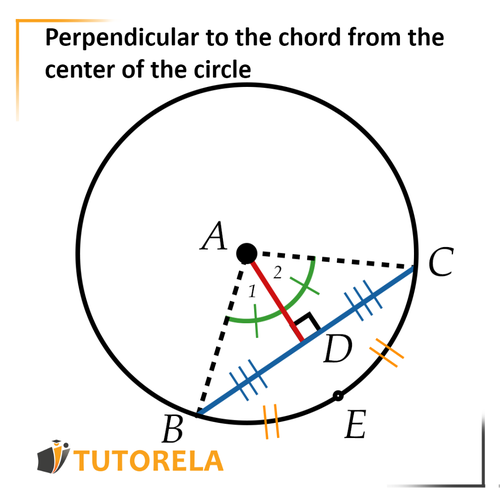
The perpendicular to the chord comes out of the center of the circle, intersecting the chord, the central angle in front of the chord and the arc in front of the chord.
Moreover, if there is a section that comes out from the center of the circle and crosses the chord, it will also be perpendicular to the chord.

We are here to present the properties of the perpendicular from the center of the circle to the chord.
First, we will remember that the perpendicular is a line that forms a $90°$ degree angle.
Let's see it in the illustration:

In front of us, there is a circle.
We will mark the center of the circle with a letter $A$
Our chord will be blue and will be called $BC$ .
The vertical, which comes out from the center of the circle and will be perpendicular to the chord $BC$ .
We will mark it in red and call it $AD$ .

Detailed explanation

Start practice

Test yourself on the parts of a circle!

Where must a point be located so that it is furthest from the center of the circle?

Practice more now

Great! Now that we understand exactly what perpendicular from the center of the circle is, we'll move on to its characteristics.
You can use these characteristics without proving them.

Characteristics of the Perpendicular to the Chord from the Center of the Circle

The perpendicular from the chord, which comes out from the center of the circle:

Join Over 30,000 Students Excelling in Math!

Endless Practice, Expert Guidance - Elevate Your Math Skills Today

Test your knowledge

Question 1

Where does a point need to be so that its distance from the center of the circle is the shortest?

Question 2

Is it correct to say:

'the circumference of a circle'?

Question 3

Is it correct to say circumference?

1) Bisects the Chord

Let's see this in the illustration:

The perpendicular $AD$ cuts the chord $BD$ in half
So that:
$BD=DC$

2) Bisects the angle in front of the chord

Let's see this in the illustration:

The perpendicular $AD$ bisects the central angle
$∡CAB$
So that:
$∢A1=∢A2$

Do you know what the answer is?

Question 1

Is it correct to say 'the area of a circle'?

Question 2

In which of the circles is the segment drawn the radius?

Question 3

Which diagram shows the radius of a circle?

3) Bisects the arc that is in front of the chord

Let's see this in the illustration:

The perpendicular $AD$ crosses the arc in front of the chord.
So that:

$BE=EC$

Please note:
Similarly, these characteristics also work in reverse, and we can say that if there is a straight line that comes out from the center of the circle and crosses the chord, then it is perpendicular to the chord.

In conclusion, a perpendicular line, coming from the center of the circle, crosses the chord, the relevant central angle, and the arc opposite the chord.
We will see all the features in an illustration:

If $AD$ is perpendicular to $BC$
Then
$∢A1=∢A2$
$BD=DC$
$BE=EC$

If you are interested in this article, you might also be interested in the following articles:

The center of the circle
Circle
Radius
Diameter
Pi
The circumference perimeter
Circular area
Arcs in a circle
Chords in a circle
Central angle in a circle
Inscribed angle in a circle
Distance from the chord to the center of the circle

In the Tutorela blog, you will find a variety of articles on mathematics.

Check your understanding

Question 1

In which of the circles is the point marked in the circle and not on the circumference?

Question 2

How many times longer is the radius of the red circle than the radius of the blue circle?

Question 3

How many times longer is the radius of the red circle, which has a diameter of 24, than the radius of the blue circle, which has a diameter of 12?

Start practice