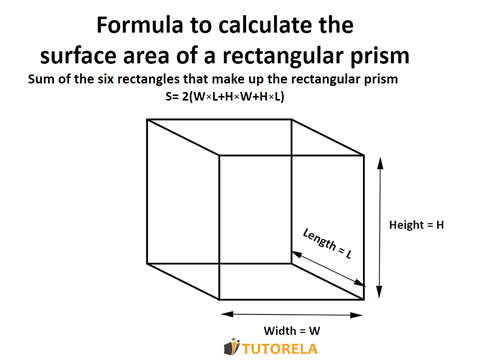
Rectangular Prisms are made up of different rectangles. When faced with an exercise or exam that asks you to calculate the surface area of a rectangular Prism, use the formula below.
How to calculate the surface area of a rectangular prism (orthohedron)
The formula: how to calculate the area of a rectangular prism (rectangular orthohedron)?
S= surface area
Test yourself on surface area of a cuboid!
Identify the correct 2D pattern of the given cuboid:
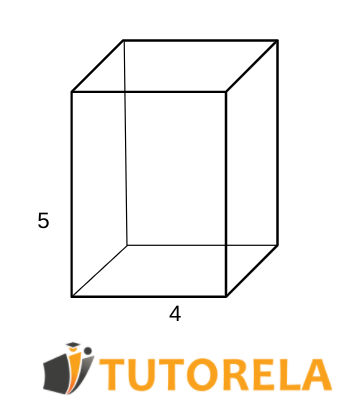
If we take as an example an orthohedron with the following characteristics, its surface area will be calculated as follows:
Width = cm
Length = cm
Height = cm
Now, we apply the formula:
Thus, by solving the exercise we will obtain that the surface area of the rectangular prism (orthohedron) is cm².
If this exercise is easy for you and you are interested in learning how to calculate the surface area of a prism, you can learn it in the following article: Surface area of triangular prisms.
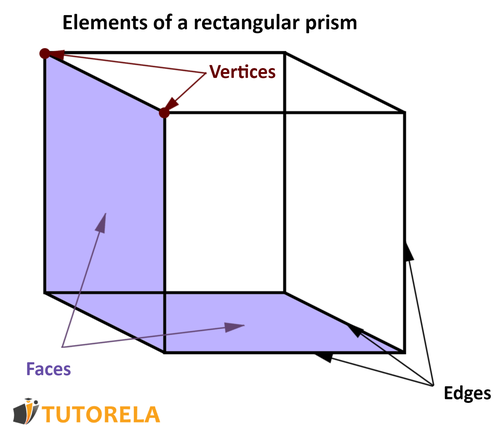
It is important to remember that in the exam the name of the shape may vary from one exercise to another.
For example: Rectangular Prism, Orthohedron and Cube.
Soit is important to remember that it is a geometric shape with faces, Edges and Vertices.
What is our conclusion?
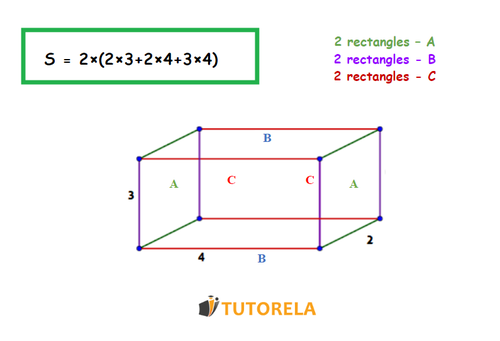
That the surface area of a rectangular prism (orthohedron) is the sum of the areas of all the rectangles that form it.
Throughout primary and secondary school, you will have to deal with exercises of all kinds related to the field of geometry. So you will need to know how to calculate the surface area of a rectangular prism. We present you the formula that will help you to do it and give you some tips to internalize the learned materials in a better way.
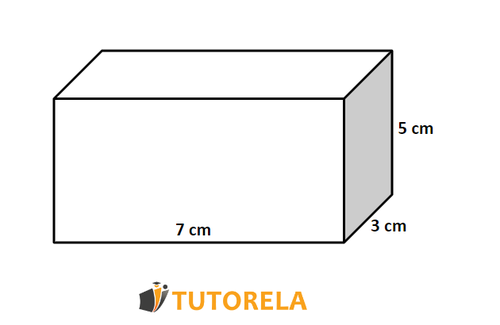
If we take as an example a rectangular prism with the following characteristics, its surface area will be calculated as follows:
Width cm
Length cm
Height cm
The surface area of the rectangular prism is:
A that the surface area of an orthohedron is the sum of the areas of all the rectangles that form it. Let's see it illustrated in the following picture:
Answer:
Thus, by solving the exercise we will obtain that the surface area of the rectangular prism is cm².
What is our conclusion?
If you are interested in this article you may also be interested in the following articles:
Orthohedron - rectangular prism
For a wide range of math articles visit Tutorela's blog.
Exercises to calculate the surface of a rectangular prism (orthohedron)
Exercise 1
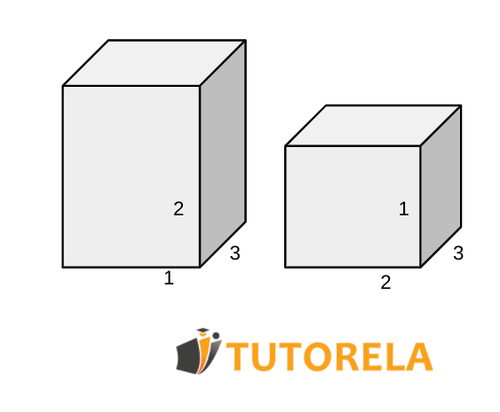
Given two orthohedra
Task:
Are the surfaces of the two orthohedra the same or different?
Solution:
Let's observe that the orthohedra are identical, they are just presented differently.
If we turn one of them upside down, it will be clear that the cubes are identical.
We can verify by calculus.
Right orthohedron :
Left Orthohedron :
Answer:
The surfaces are equal.
A cuboid is shown below:
What is the surface area of the cuboid?
Calculate the surface area of the orthohedron below using the data in the diagram.
Look at the the cuboid below.
What is its surface area?
Exercise 2
Given that the area of the orthohedron is equal to cm².
The height of the orthohedron is equal to cm and the width is cm.
Calculate the volume of the orthohedron
Task:
Calculate the volume of the orthohedron.
Solution:
Area = cm²
Length = cm
Width = cm
Height =
Replace the height by
/ :divide into
The length is equal to cm.
We replace it in the volume formula:
Answer:
The volume of the orthohedron is equal to cm³.
Exercise 3
Given a cube with the following information:
Width cm
Length cm
Height cm
How to calculate the surface area of the cube.
Answer:
The surface area of the cube is: cm².
Look at the cuboid below.
What is its surface area?
What is the surface area of the cuboid in the figure?
A cuboid has the dimensions shown in the diagram below.
Which rectangles form the cuboid?
Exercise 4
Given a rectangular prism with the following information:
Width cm
Length cm
Height cm
How to calculate the surface area of the rectangular prism.
Answer:
cm²
Exercise 5
Given a rectangular prism with the following information:
Width cm
Length cm
Height cm
How to calculate the surface area of the rectangular prism.
Answer:
The surface area of the rectangular prism is: cm².
Look at the cuboid below.
What is the surface area of the cuboid?
The surface area of a cube is 24 cm². How long is the cube's side?
The surface area of the cuboid shown below is 147 cm².
What are the dimensions of the cuboid that are not labelled in the drawing?
Review questions
How do you calculate the total area of a rectangular prism?
To calculate the total area of a rectangular prism, we have to calculate the areas of each of its faces (6 faces) and then add the area of all of them to obtain the total area.
What is the formula for finding the area of a prism?
Factoring the
where:
Surface area
length
width
height
Look at the cuboid of the figure.
Its surface area is 122 cm².
What is the width of the cuboid?
Calculate the surface area of the box shown in the diagram.
Pay attention to the units of measure!
Given the cuboid whose square base is of size 25 cm²,
The height of the cuboid is 3 cm,
What is the surface area of the cuboid?
How to calculate the area and volume of a rectangular prism?
The area of a rectangular prism is calculated with the formula:
While the volume is calculated with the following formula:
Example
Let the following rectangular prism have the following dimensions
Width
Length
Height
Let's calculate the area with the formula
Now we calculate the volume
Result
How do you calculate the area of a rectangular box?
To calculate the area of a rectangular box we add the areas of its six faces, or by using the following formula:
Where:
Surface area
length
width
height
A cuboid has a surface area of 102.
Calculate X.
A rectangular prism has a square base measuring 25 cm.
It has a height is equal to 3 cm.
Calculate the surface area of the rectangular prism.
Identify the correct 2D pattern of the given cuboid:
Examples with solutions for Surface Area of a Cuboid
Exercise #1
Identify the correct 2D pattern of the given cuboid:
Step-by-Step Solution
Let's go through the options:
A - In this option, we can observe that there are two flaps on the same side.
If we try to turn this net into a box, we should obtain a box where on one side there are two faces one on top of the other while the other side is "open",
meaning this net cannot be turned into a complete and full box.
B - This net looks valid at first glance, but we need to verify that it matches the box we want to draw.
In the original box, we see that we have four flaps of size 9*4, and only two flaps of size 4*4,
if we look at the net we can see that the situation is reversed, there are four flaps of size 4*4 and two flaps of size 9*4,
therefore we can conclude that this net is not suitable.
C - This net at first glance looks valid, it has flaps on both sides so it will close into a box.
Additionally, it matches our drawing - it has four flaps of size 9*4 and two flaps of size 4*4.
Therefore, we can conclude that this net is indeed the correct net.
D - In this net we can see that there are two flaps on the same side, therefore this net will not succeed in becoming a box if we try to create it.
Answer
Exercise #2
A cuboid is shown below:
What is the surface area of the cuboid?
Video Solution
Step-by-Step Solution
Remember that the formula for the surface area of a cuboid is:
(length X width + length X height + width X height) 2
We input the known data into the formula:
2*(3*2+2*5+3*5)
2*(6+10+15)
2*31 = 62
Answer
62
Exercise #3
Calculate the surface area of the orthohedron below using the data in the diagram.
Video Solution
Step-by-Step Solution
To solve this problem, we'll utilize the formula for the surface area of a cuboid. The steps are as follows:
- Step 1: Identify the dimensions from the problem. The dimensions provided are , , and .
- Step 2: Apply the surface area formula for a cuboid. The formula is: where , , and are the dimensions of the cuboid.
- Step 3: Substitute the known values into the formula:
- Step 4: Calculate each term inside the parentheses: - - -
- Step 5: Sum the results from Step 4:
- Step 6: Multiply the sum by 2 to find the total surface area:
Thus, after performing the necessary calculations, the surface area of the orthohedron is square units.
Answer
62
Exercise #4
Look at the the cuboid below.
What is its surface area?
Video Solution
Step-by-Step Solution
First, we recall the formula for the surface area of a cuboid:
(width*length + height*width + height*length) *2
As in the cuboid the opposite faces are equal to each other, the given data is sufficient to arrive at a solution.
We replace the data in the formula:
(8*5+3*5+8*3) *2 =
(40+15+24) *2 =
79*2 =
158
Answer
158
Exercise #5
Look at the cuboid below.
What is its surface area?
Video Solution
Step-by-Step Solution
We identified that the faces are
3*3, 3*11, 11*3
As the opposite faces of an cuboid are equal, we know that for each face we find there is another face, therefore:
3*3, 3*11, 11*3
or
(3*3, 3*11, 11*3 ) *2
To find the surface area, we will have to add up all these areas, therefore:
(3*3+3*11+11*3 )*2
And this is actually the formula for the surface area!
We calculate:
(9+33+33)*2
(75)*2
150
Answer
150
More Questions
Surface Area of a Cuboid
- Calculate Cube Side Length from Surface Area: 24 cm² Problem
- Surface Area of Rectangular Prism: Express in Terms of X (3×5×X)
- Calculate Cube Surface Area: Express Total Area in Terms of Side Length 'a'
- Surface Area of a Rectangular Prism: Express in Terms of Variable 'a' (5×1×a)
- Surface Area of Rectangular Prism: Express in Terms of a, b, and c
- Area
- The Application of the Pythagorean Theorem to an Orthohedron or Cuboid
- Rectangle
- Calculating the Area of a Rectangle
- The perimeter of the rectangle
- Congruent Rectangles
- Perimeter
- Cylinder Surface Area
- Cylinder Volume
- Cuboids
- Cubes
- How to calculate the volume of a rectangular prism (orthohedron)
- Lateral surface area of a rectangular prism
- Right Triangular Prism
- Bases of the Right Triangular Prism
- The lateral faces of the prism
- Lateral Edges of a Prism
- Height of a Prism
- The volume of the prism
- Surface area of triangular prisms
- Areas of Polygons for 7th Grade
- How do we calculate the area of complex shapes?
- How do we calculate the perimeter of polygons?









