We learned in the previous article about the number line AND we also talked about positive and negative numbers. In this article we move on and call them integers.
Signed Numbers Practice Problems: Positive & Negative Integers
Master signed numbers with step-by-step practice problems. Learn to compare, order, and perform operations with positive and negative integers effectively.
πWhat You'll Master with Signed Numbers Practice
- Compare positive and negative integers using inequality symbols correctly
- Order signed numbers from least to greatest on the number line
- Add and subtract positive and negative integers with confidence
- Apply integer rules to solve real-world problems involving temperatures and elevations
- Identify which numbers are integers versus decimals and fractions
- Determine true or false statements about signed number properties
Understanding Signed Numbers (Positive and Negative)
Complete explanation with examples
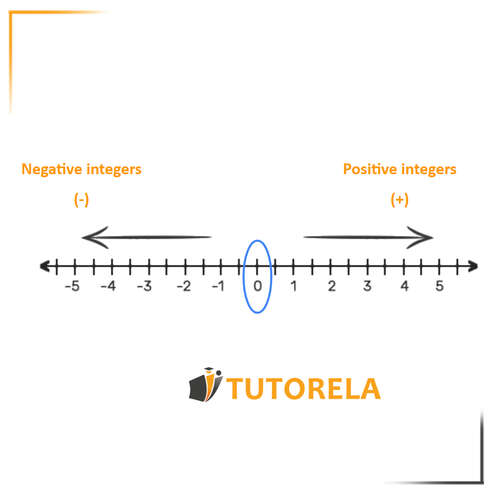
What are integers?
The term "integer" refers to any number to the left of which there is a plus sign (+) or minus sign (-).
- The plus sign ( ) indicates that the number is positive (greater than zero). The minus sign (-) means that the number is negative (less than zero).
- When a number appears without one of these two signs, it means that the number is positive.
- Exception: The number . Zero is the only number that is neither positive nor negative. It is possible to write "" or "", but in this case the signs will have no meaning.
Practice Signed Numbers (Positive and Negative)
Test your knowledge with 19 quizzes
Fill in the missing number:
\( 10\cdot?=-100 \)
Examples with solutions for Signed Numbers (Positive and Negative)
Step-by-step solutions included
Exercise #1
Determine the resulting sign of the following exercise:
Step-by-Step Solution
When there is no minus or plus sign before the numbers, we usually assume that these are positive numbers as shown below:
(+1/4)*(+1/2)=
The dot in the middle represents multiplication:
So the question in other words is - what happens when we multiply two positive numbers together?
We know that two positive integers when multiplied result in a positive integer:
Therefore the answer is "positive".
Answer:
Positive
Video Solution
Exercise #2
What will be the sign of the result of the next exercise?
Step-by-Step Solution
To determine the sign of the expression , we follow these logical steps:
- Step 1: Identify the signs of the numbers involved. Both numbers and are negative.
- Step 2: Apply the rule for multiplication of signed numbers: The product of two numbers with the same sign (both negative) is always positive.
Therefore, the sign of the result for the expression is Positive.
Answer:
Positive
Video Solution
Exercise #3
What will be the sign of the result of the next exercise?
Step-by-Step Solution
To solve the exercise you need to remember an important rule: Multiplying a positive number by a negative number results in a negative number.
Therefore, if we multiply negative 2 by 2 the result will be negative 4.
That is, the result is negative.
Answer:
Negative
Video Solution
Exercise #4
What will be the sign of the result of the next exercise?
Step-by-Step Solution
It's important to remember: when we multiply a negative by a negative, the result is positive!
You can use this guide:
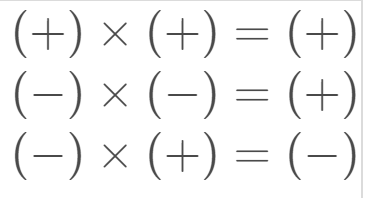
Answer:
Positive
Video Solution
Exercise #5
What will be the sign of the result of the next exercise?
Step-by-Step Solution
Let's recall the law:
Therefore, the sign of the exercise result will be positive:
Answer:
Positive
Video Solution
Frequently Asked Questions
What are signed numbers and how do they differ from regular numbers?
+Signed numbers are integers with either a positive (+) or negative (-) sign in front of them. When no sign appears, the number is assumed to be positive. Zero is neither positive nor negative and is the only exception to this rule.
How do you compare positive and negative integers?
+Follow these three rules: 1) Any positive number is always greater than any negative number, 2) For two positive numbers, the one with the larger absolute value is greater, 3) For two negative numbers, the one with the smaller absolute value is greater (closer to zero).
What happens when you add two negative integers?
+When adding two negative integers, you add their absolute values together and keep the negative sign. For example: (-5) + (-3) = -8. The result is always negative when adding two negative numbers.
How do you subtract a negative number from a positive number?
+When subtracting a negative number, it becomes addition. The rule is: minus times minus equals plus. For example: 12 - (-2) = 12 + 2 = 14. This is because subtracting a negative is the same as adding a positive.
Which numbers are NOT considered integers?
+Numbers that are NOT integers include: decimals (like 1.5 or -3.7), fractions (like 2/3 or -5/8), and irrational numbers (like Ο). Integers must be whole numbers without decimal points or fractional parts.
Where do negative numbers appear on the number line?
+All negative numbers appear to the left of zero on the number line, while positive numbers appear to the right of zero. The further left a negative number is, the smaller its value becomes.
Can zero be positive or negative?
+No, zero is neither positive nor negative. While you can write +0 or -0, these signs have no mathematical meaning. Zero is the only number that sits exactly in the middle of the number line.
How do you solve problems with multiple signed numbers?
+First, simplify the signs by converting double negatives to positives. Then group positive and negative terms separately. Finally, subtract the smaller sum from the larger sum and keep the sign of the larger group.