In previous articles, we have studied real numbers and the grouping of terms, as well as the order of mathematical operations with parentheses. In this article, we move forward and combine these topics in order to understand when and how we can eliminate parentheses in real numbers.
Elimination of Parentheses Practice Problems & Solutions
Master eliminating parentheses in real numbers with step-by-step practice problems. Learn sign rules, solve equations, and build confidence with guided exercises.
πPractice Eliminating Parentheses with Interactive Problems
- Apply the four sign rules: ++, --, +-, and -+ combinations
- Remove parentheses correctly using mathematical elimination rules
- Solve real number expressions with multiple parentheses groups
- Master positive and negative number operations without parentheses
- Complete multi-step problems involving parentheses elimination
- Build confidence with graduated difficulty practice exercises
Understanding Elimination of Parentheses in Real Numbers
Complete explanation with examples
What does the elimination of parentheses in real numbers mean?
When we perform grouping of like terms ("addition and subtraction") with real numbers, we confine the real number within parentheses.
Parentheses can be removed but when eliminating them, the following rules must be remembered:
Β
Β
Β
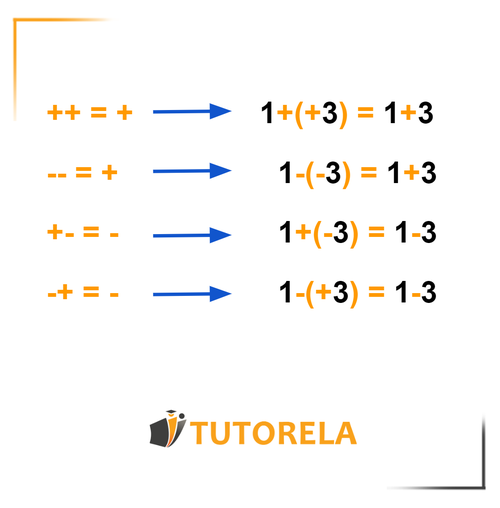
Practice Elimination of Parentheses in Real Numbers
Test your knowledge with 3 quizzes
\( (+0.5)+(+\frac{1}{2})= \)
Examples with solutions for Elimination of Parentheses in Real Numbers
Step-by-step solutions included
Exercise #1
What is the inverse number of
Step-by-Step Solution
To solve the problem of finding the opposite number of , we will use the concept of opposite numbers:
- Step 1: Identify the given number, which is .
- Step 2: Determine the opposite number by changing the sign. The opposite of is calculated as follows:
The opposite of a negative number is its positive counterpart. So, the opposite of is .
Therefore, the answer is .
Answer:
Video Solution
Exercise #2
What is the inverse number of
Step-by-Step Solution
To solve this problem, we'll follow these steps:
- Step 1: Identify the given number.
- Step 2: Find its opposite by changing the sign.
Now, let's work through each step:
Step 1: The problem gives us the number .
Step 2: The opposite of a positive number is the same number with a negative sign.
Thus, the opposite of is .
Therefore, the opposite number of is .
Answer:
Video Solution
Exercise #3
What is the additive inverse number of
Step-by-Step Solution
To solve this problem, we'll follow these steps:
- Step 1: Identify the given number
- Step 2: Apply the definition of an opposite number
- Step 3: Conclude with the opposite number
Now, let's work through each step with detailed explanations:
Step 1: We are given the number . This is a positive integer.
Step 2: The definition of an opposite number states that the opposite of any number is . Here, .
Step 3: Using the definition, the opposite number of is calculated as .
Therefore, the solution to the problem is .
Answer:
Video Solution
Exercise #4
What is the inverse number of
Step-by-Step Solution
To determine the opposite number of , we will simply change its sign, following these steps:
- Step 1: Identify the given number, which is .
- Step 2: Change the sign of to find its opposite. Since is positive, its opposite will be negative.
By changing the sign of , we get . Therefore, the opposite number of is .
In conclusion, the solution to the problem is .
Answer:
Video Solution
Exercise #5
What is the inverse number of
Step-by-Step Solution
To determine the opposite number of , we need to understand what the opposite of a number means in mathematics.
The opposite of a number is simply a number with the same magnitude but the opposite sign. For any real number , its opposite is . When is already negative, its opposite is positive.
Given the number , we will apply the following steps:
- Identify the sign and magnitude: The given number is , a negative fraction.
- Apply sign change: The opposite is simply the positive version of , which is .
Thus, the opposite of is .
Therefore, the correct answer is .
Answer:
Video Solution
Frequently Asked Questions
What are the four rules for eliminating parentheses in real numbers?
+The four essential rules are: ++ = + (positive plus positive equals positive), -- = + (negative minus negative equals positive), +- = - (positive plus negative equals negative), and -+ = - (negative minus positive equals negative). These rules help you correctly remove parentheses from mathematical expressions.
How do you eliminate parentheses with negative signs?
+When eliminating parentheses with negative signs, remember that subtraction gives you the opposite number. For example, -(-6) becomes +6, and -(+6) becomes -6. The minus sign flips the sign of the number inside the parentheses.
What is the correct order for solving expressions with parentheses?
+Follow these steps: 1) First eliminate all parentheses using sign rules, 2) Perform operations from left to right, 3) Handle addition and subtraction in order. For example: (-5)+(+35)-(-22) becomes -5+35+22 = 52.
When can you omit the plus sign in mathematical expressions?
+You can only omit the plus sign when the positive number is the first in the sequence. For example, write 50-20 instead of +50-20, but you must keep the plus in expressions like -3+4 where the positive number comes after a negative.
What are common mistakes when eliminating parentheses?
+Common errors include: β’ Forgetting to change signs when subtracting negative numbers β’ Incorrectly applying sign rules like confusing +- with -- β’ Removing plus signs from numbers that aren't first in the sequence β’ Not following the proper order of operations after parentheses removal
How do you solve complex expressions with multiple parentheses?
+Work systematically: first eliminate all parentheses using sign rules, then solve from left to right. For example: (+58)-(-34)+(+9)-(+5)+(-2) becomes 58+34+9-5-2 = 94. Always apply parentheses elimination rules before performing arithmetic operations.
Why is understanding parentheses elimination important in algebra?
+Mastering parentheses elimination is fundamental for algebra success. It prepares you for solving equations, simplifying expressions, and working with polynomials. This skill builds the foundation for more advanced topics like factoring and solving systems of equations.
How do you check if you eliminated parentheses correctly?
+Verify your work by: 1) Checking that you applied the correct sign rule for each parentheses pair, 2) Ensuring positive numbers are written without + signs only when they're first, 3) Solving the original expression and your simplified version to confirm they equal the same result.