Table of Values Practice Problems with Step-by-Step Solutions

Master creating value tables for linear and quadratic functions. Practice plotting graphs from tables with detailed solutions and examples for algebra students.

📚Master Value Tables Through Interactive Practice

Create accurate value tables for linear functions like Y = X + 2
Plot coordinate points from value tables onto graph axes
Determine linear equations from given value table data
Connect plotted points to draw complete function graphs
Solve for Y values when given specific X inputs
Identify patterns and relationships between X and Y coordinates

Understanding Table of Values

Complete explanation with examples

A value table is the "preparatory work" that we are often asked to do before producing a graphical representation. Therefore, it is an inseparable part of the subject of graphs in general and the topic of functions in particular.

What is a Value Table?

A value table is actually a database, on which a discrete or continuous graph is based.
The data table lists the corresponding value of $Y$ for each $X$ .
The value table allows you to project and draw the graph conveniently and efficiently.
Below is an example of a value table for the function $Y=X+2$

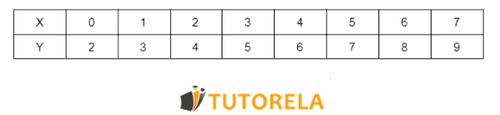
Image -- an example of a value table for the function Y = X + 21

Based on this value table, the following linear function can be plotted:

Detailed explanation

Practice Table of Values

Test your knowledge with 2 quizzes

Find $$ y $$ when $$ x=2 $$

$y=\frac{2}{5}x+2$

Examples with solutions for Table of Values

Step-by-step solutions included

Exercise #1

Calculate y given that $x=2$ and $y=x$ .

Step-by-Step Solution

We are given the equation y=x

We are also given the value of x,

x=2

Therefore, we will insert the given value into the equation

y=2

And that's the solution!

Answer:

$2$

Video Solution

Exercise #2

Find a y when $x=2$

$y=5x$

Step-by-Step Solution

To solve this problem, we'll follow these steps:

Step 1: Identify the given equation $y = 5x$ .
Step 2: Substitute the value $x = 2$ into the equation.
Step 3: Calculate the value of $y$ .

Now, let's work through each step:
Step 1: We start with the equation $y = 5x$ .
Step 2: Substitute $x = 2$ into this equation:
$y = 5 \times 2$ .
Step 3: Perform the multiplication:
$y = 10$ .

Therefore, the solution to the problem is $y = 10$ .

Answer:

Video Solution

Exercise #3

Find a y when x=2

$y=\frac{1}{2}x$

Step-by-Step Solution

To solve this problem, we will follow these steps:

Step 1: Substitute the given value of $x$ into the equation.
Step 2: Perform the calculations to find $y$ .

Now, let's work through each step:
Step 1: The equation provided is $y = \frac{1}{2}x$ . We need to find the value of $y$ when $x = 2$ .
Step 2: Substitute $x = 2$ into the equation:

$y = \frac{1}{2} \times 2$

Simplifying this expression gives:

$y = \frac{2}{2}$

Therefore,

$y = 1$ .

The calculated value of $y$ is $1$ .

Answer:

$1$

Video Solution

Exercise #4

Find a y when x=2

$y=x-8$

Step-by-Step Solution

To solve the problem, we will follow these steps:

Step 1: Substitute the given value of $x$ into the equation $y = x - 8$ .
Step 2: Simplify the expression to find the corresponding value of $y$ .

Now, let's apply these steps:

Step 1: Given the equation $y = x - 8$ , we substitute $x = 2$ :
$\begin{aligned} y &= 2 - 8 \end{aligned}$

Step 2: Simplify the expression:
$\begin{aligned} y &= -6 \end{aligned}$

Thus, the value of $y$ when $x = 2$ is $-6$ .

Therefore, the solution to the problem is $y = -6$ .

Answer:

$-6$

Video Solution

Exercise #5

Calculate y given that $X=2$ and $y=0.8x$ .

Step-by-Step Solution

To solve this problem, we will follow these steps:

Step 1: Identify the given information
Step 2: Apply the formula
Step 3: Perform the calculation

Now, let's work through each step:
Step 1: The problem gives us that $x = 2$ and the relationship between $y$ and $x$ is $y = 0.8x$ .
Step 2: We will use the formula $y = 0.8 \times x$ .
Step 3: Substituting $x = 2$ into the formula, we get $y = 0.8 \times 2$ .

The calculation is as follows:
$y = 0.8 \times 2 = 1.6$ .

Therefore, the solution to the problem is $y = 1.6$ .

Answer:

1.6

Video Solution

Frequently Asked Questions

Everything you need to know about Table of Values

What is a value table in math and why do I need it?

A value table is a systematic way to organize X and Y coordinate pairs before graphing a function. It serves as preparatory work that makes plotting graphs easier and more accurate by providing specific points to plot on the coordinate plane.

How do I create a value table for a linear function?

To create a value table: 1) Choose simple X values (like -2, -1, 0, 1, 2), 2) Substitute each X value into your equation, 3) Calculate the corresponding Y value, 4) Record each (X,Y) pair in your table. Use small numbers to make calculations easier.

What's the difference between value tables for linear and quadratic functions?

Linear function tables show a constant rate of change between Y values, while quadratic function tables show increasing or decreasing rates of change. Linear functions create straight lines when graphed, while quadratic functions create parabolas.

How many points do I need in my value table to graph a function?

For linear functions, you technically need only 2 points, but 3-5 points are recommended for accuracy. For quadratic functions, use at least 5-7 points including the vertex to capture the parabola's shape properly.

Can I determine a function's equation from its value table?

Yes! For linear functions, look for the constant difference between Y values. If Y increases by the same amount for each unit increase in X, that's your slope. The Y-intercept is the Y value when X equals zero.

What are common mistakes when creating value tables?

Common errors include: • Calculation mistakes when substituting values • Choosing X values that are too large or complex • Not organizing data clearly in rows and columns • Forgetting to check work by verifying a few calculations • Mixing up X and Y coordinates when plotting

How do I use a value table to plot points on a graph?

Each row in your table represents one coordinate point (X,Y). Locate the X value on the horizontal axis, then move vertically to the Y value on the vertical axis. Mark the intersection point, then repeat for all table entries before connecting the points.

Why should I use rulers when drawing graphs from value tables?

Using rulers ensures precision and accuracy when connecting plotted points. This is especially important for linear functions where the line should be perfectly straight, and helps create professional-looking graphs that clearly demonstrate mathematical relationships.

Continue Your Math Journey

Master Table of Values first, then advance to these related topics that build on your fraction skills

Topics Learned in Later Sections

Numerical Value

Practice by Question Type

Choose your preferred learning style and practice format for fraction problems

Completing the table