Algebraic Expressions - Examples, Exercises and Solutions

When a problem is presented to us in writing, we can convert it into mathematical language (also called algebraic language) by transforming it into an algebraic expression. But what are algebraic expressions?

Variable: This is a letter that represents a numerical value, for example $X$ or $Y$ . This letter refers to an unknown numerical value that we must work out. For example: if $X+5=8$ , then we can conclude that the numerical value of $X$ is $3$ .

An algebraic expression is a combination of numbers and letters (representing unknown numbers) that includes operations such as addition, subtraction, multiplication, division, etc.

Each element of an algebraic expression is called an algebraic term, be it a variable, a constant, or a combination of a coefficient and one or more variables. If the expression contains only one term, it is known as a monomial, while those that contain two or more terms are polynomials.

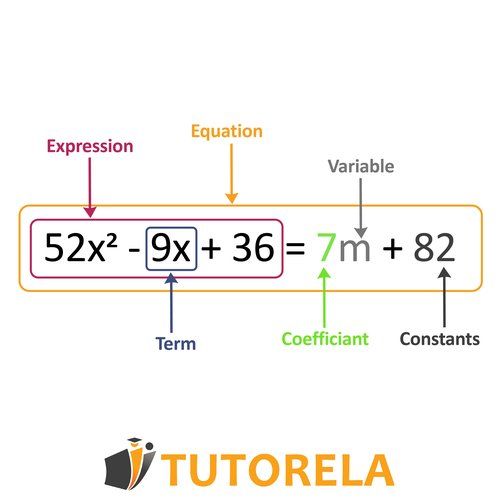
There is no limitation to the amount of constant numbers, unknown variables, or operations that can appear in an algebraic expression. In addition, there does not always have to be a variable in the algebraic expression, although it will always have a certain numerical value.

Detailed explanation

Practice Algebraic Expressions

Question 1

$18x-7+4x-9-8x=\text{?}$

Question 2

$7.3\cdot4a+2.3+8a=\text{?}$

Question 3

$\frac{8x^2}{4x}+3x=$

Question 4

$$ Simplifica la expresión:

$2x^3\cdot x^2-3x\cdot x^4+6x\cdot x^2-7x^3\cdot 5=$

Question 5

$\frac{9m}{3m^2}\times\frac{3m}{6}=$

Examples with solutions for Algebraic Expressions

Exercise #1

$18x-7+4x-9-8x=\text{?}$

Video Solution

Step-by-Step Solution

To solve the exercise, we will reorder the numbers using the substitution property.

$18x-8x+4x-7-9=$

To continue, let's remember an important rule:

1. It is impossible to add or subtract numbers with variables.

That is, we cannot subtract 7 from 8X, for example...

We solve according to the order of arithmetic operations, from left to right:

$18x-8x=10x$ $10x+4x=14x$ $-7-9=-16$ Remember, these two numbers cannot be added or subtracted, so the result is:

$14x-16$

Answer

$14x-16$

Exercise #2

$7.3\cdot4a+2.3+8a=\text{?}$

Video Solution

Step-by-Step Solution

It is important to remember that when we have numbers and variables, it is impossible to add or subtract them from each other.

We group the elements:

$7.3×4a + 2.3 + 8a =$

$29.2a + 2.3 + 8a =$

$37.2a + 2.3$

And in this exercise, this is the solution!

You can continue looking for the value of a.

But in this case, there is no need.

Answer

$37.2a+2.3$

Exercise #3

$\frac{8x^2}{4x}+3x=$

Video Solution

Step-by-Step Solution

Let's break down the fraction's numerator into an expression:

$8x^2=4\times2\times x\times x$

And now the expression will be:

$\frac{4\times2\times x\times x}{4x}+3x=$

Let's reduce and get:

$2x+3x=5x$

Answer

$5x$

Exercise #4

Simplifica la expresión:

$2x^3\cdot x^2-3x\cdot x^4+6x\cdot x^2-7x^3\cdot 5=$

Video Solution

Step-by-Step Solution

We'll use the law of exponents for multiplication between terms with identical bases:

$a^m\cdot a^n=a^{m+n}$ We'll apply this law to the expression in the problem:

$2x^3\cdot x^2-3x\cdot x^4+6x\cdot x^2-7x^3\cdot 5=2x^{3+2}-3x^{1+4}+6x^{1+2}-35x^3$ When we apply the above law to the first three terms from the left, while remembering that any number can always be considered as that number raised to the power of 1:

$a=a^1$ And in the last term we performed the numerical multiplication,

We'll continue and simplify the expression we got in the last step:

$2x^{3+2}-3x^{1+4}+6x^{1+2}-35x^3=2x^5-3x^5+6x^3-35x^3=-x^5-29x^3$ Where in the first stage we simplified the expressions in the exponents of the terms in the expression and in the second stage we combined like terms,

Therefore the correct answer is answer A.

Answer

$-x^5-29x^3$

Exercise #5

$\frac{9m}{3m^2}\times\frac{3m}{6}=$

Video Solution

Step-by-Step Solution

According to the laws of multiplication, we must first simplify everything into one exercise:

$\frac{9m\times3m}{3m^2\times6}=$

We will simplify and get:

$\frac{9m^2}{m^2\times6}=$

We will simplify and get:

$\frac{9}{6}=$

We will factor the expression into a multiplication:

$\frac{3\times3}{3\times2}=$

We will simplify and get:

$\frac{3}{2}=1.5$

Answer

$0.5m$

Question 1

$3x+4x+7+2=\text{?}$

Question 2

$3z+19z-4z=\text{?}$

Question 3

Are the expressions the same or not?

$$ 20x $$

$2\times10x$

Question 4

Are the expressions the same or not?

$$ 3+3+3+3 $$

$3\times4$

Question 5

Are the expressions the same or not?

$$ 18x $$

$$ 2+9x $$

Exercise #6

$3x+4x+7+2=\text{?}$

Video Solution

$$ x+x= $$

Question 2

$$ 5+8-9+5x-4x= $$

Question 3

$$ 5+0+8x-5= $$

Question 4

$$ 11+5x-2x+8= $$

Answer

$11a+17b$