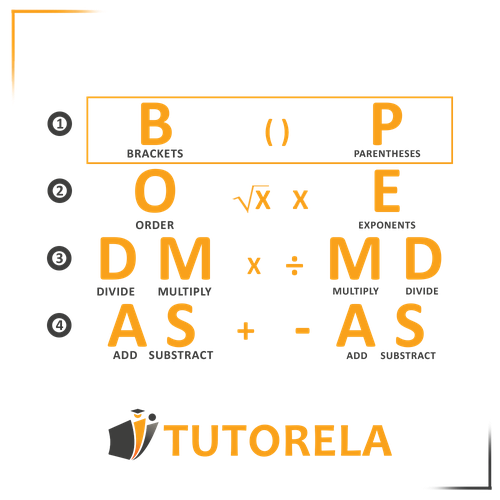
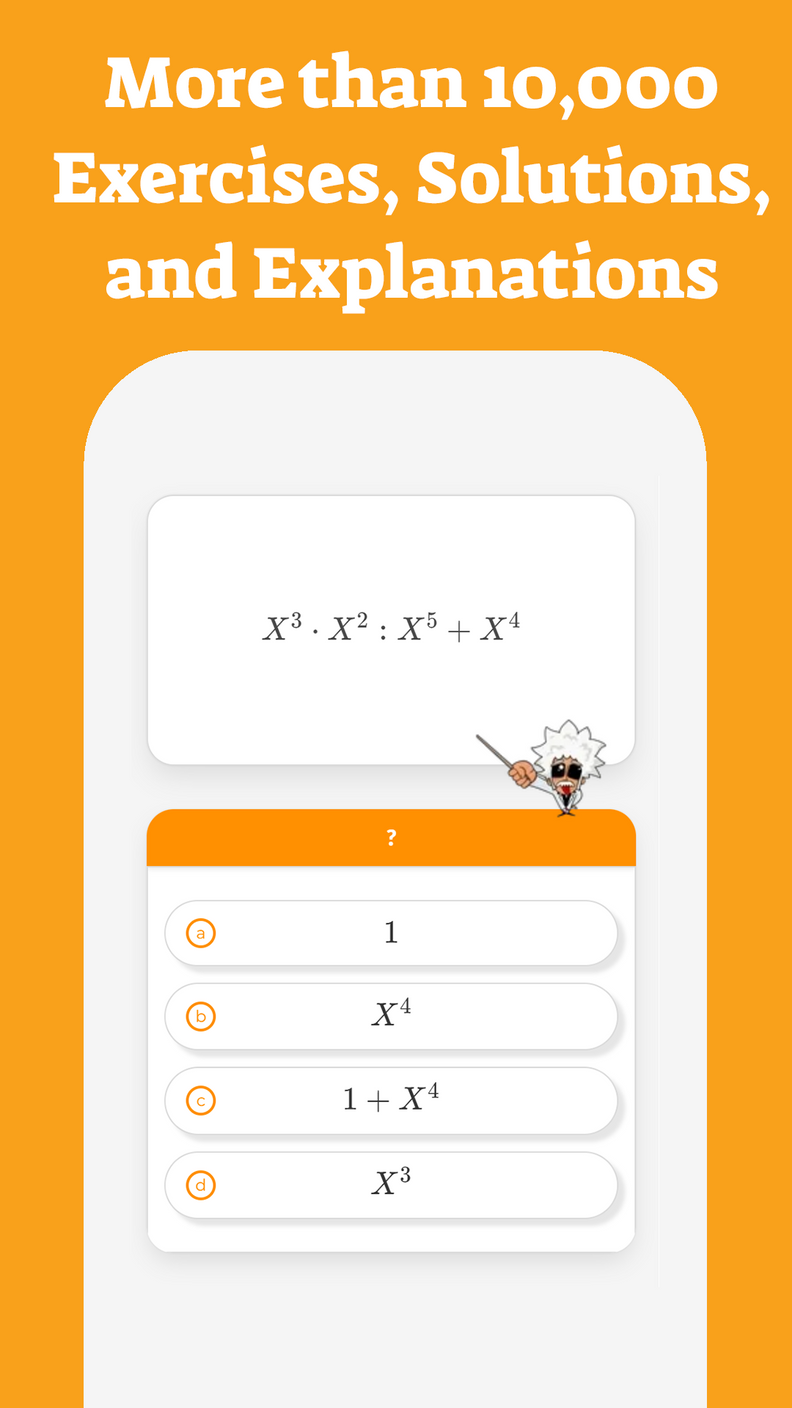
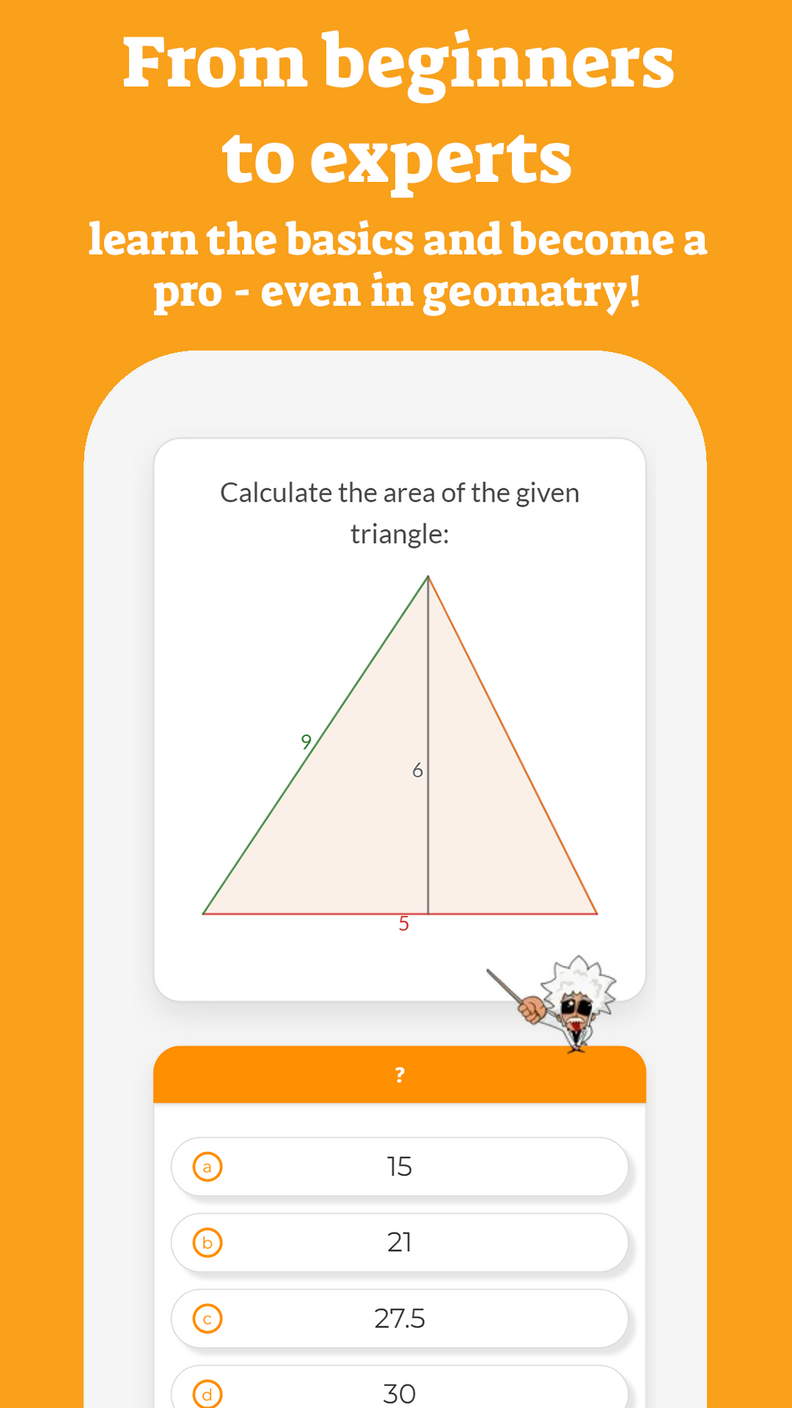
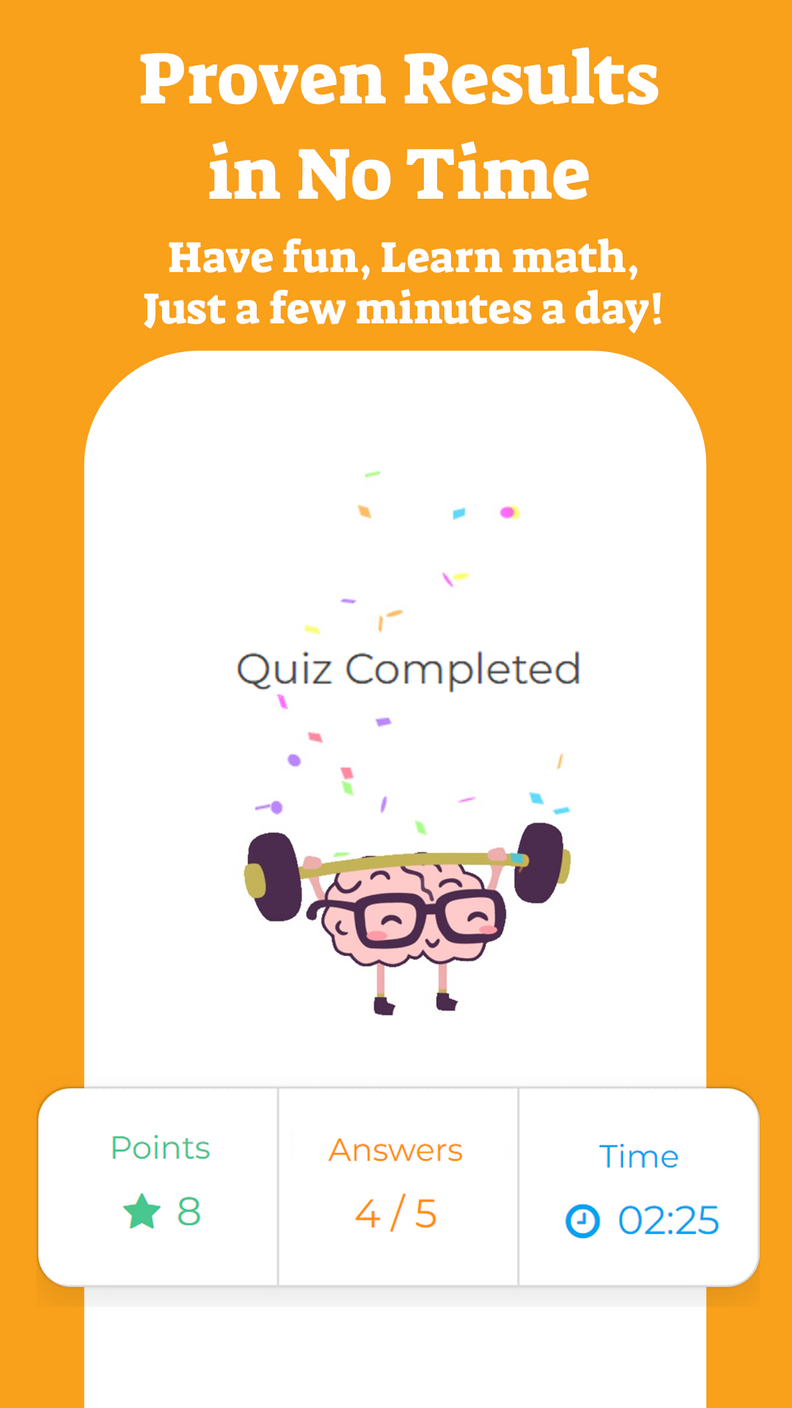
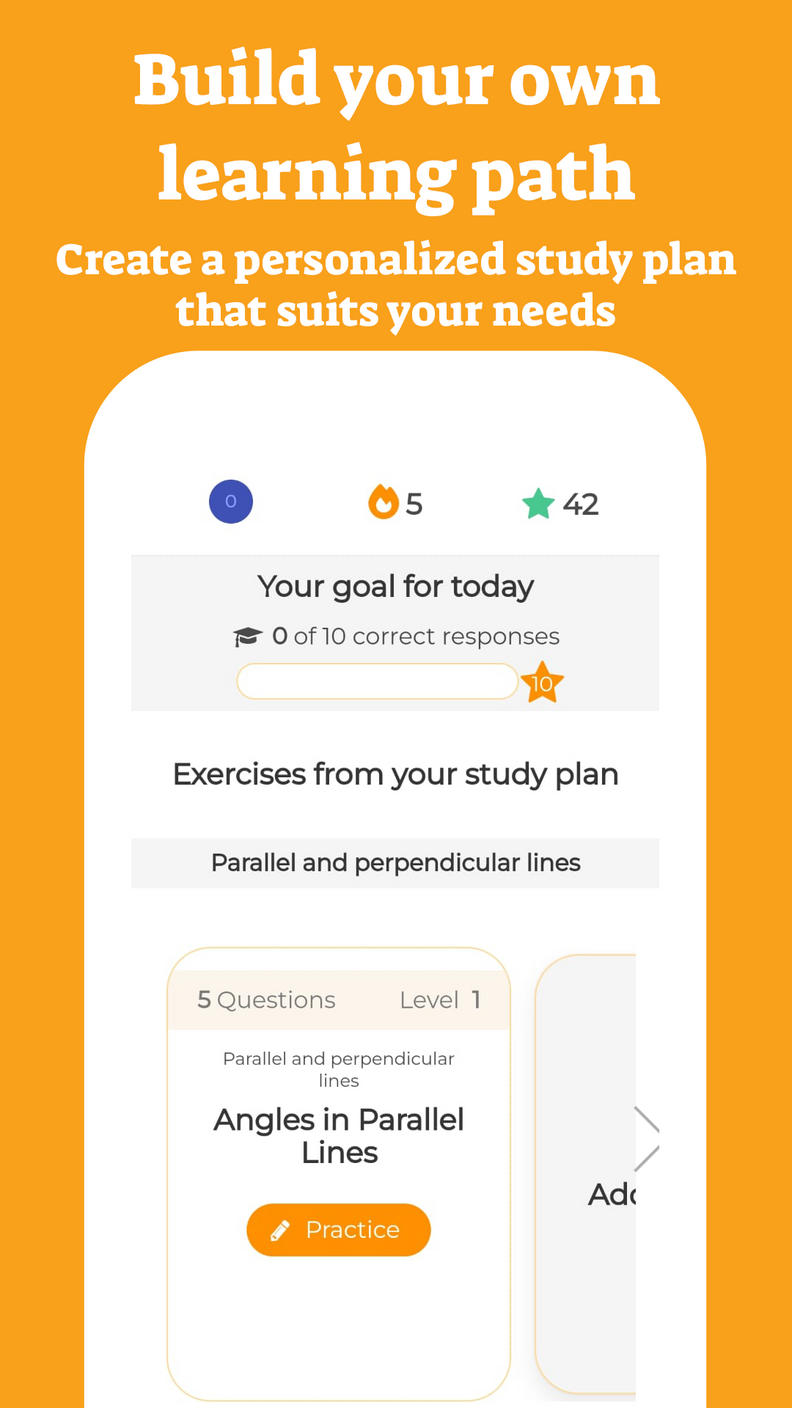
Order of Operations with Parentheses

In previous articles, we have seen what is the order of operations for addition, subtraction, multiplication, and division and also the order we must follow when there are exponents.

When the exercise we need to solve includes parentheses, we always (always!) start with the operation contained within them.

Reminder: when an exercise presents operations that have the same precedence, that is, multiplications and divisions or additions and subtractions, we will solve the exercise from left to right.

Detailed explanation

Start practice

Test yourself on parentheses in advanced order of operations!

Solve the following:

$$ 18-(3+3)= $$

Practice more now

Below, we present to you some examples

Example 1

$4+(6:2)=$
In this exercise, we will start by solving the operation inside the parentheses, and then the rest:
$4+(6:2)=4+(3)= 4+3 = 7$

Join Over 30,000 Students Excelling in Math!

Endless Practice, Expert Guidance - Elevate Your Math Skills Today

Test your knowledge

Question 1

$$ 10-(10-4):2= $$

Question 2

$$ 10-(10-4):2= $$

Question 3

$$ 18-(3+3)= $$

Example 2

$5+8\cdot3-(8:4)=$
We'll start by solving the operation inside the parentheses:
$5+8\cdot3-2=$
Next, we continue with the multiplications:
$5+24-2=$
Finally, we add and subtract:
$5+24-2=27$

Example 3

$1+9\cdot15-(9:3)=$
We'll start by solving the operation inside the parentheses:
$1+9\cdot15-3=$
Next, we continue with the multiplications:
$1+135-3=$
Finally, we add and subtract:
$1+135-3=133$

Do you know what the answer is?

Question 1

$187\times(8-5)=$

Question 2

$$ (29-4):5= $$

Question 3

$(7+2)\times(3+8)=$

Example 4

$(21+3)\cdot2\operatorname{\cdot}4-(22:2)=$

We will start by solving the operation inside the parentheses:
$24\cdot2\operatorname{\cdot}4-11=$

Next, we continue with the multiplications:
$48\operatorname{\cdot}4-11=$

$192-11=$

Finally, we add and subtract:
$192-11=181$

Example 5

$(1+9)+(15\cdot8)-(8:2)=$

Let's start by solving the operation inside the parentheses:
$(10)+(120)-(4)=$

Finally, we add and subtract:
$10+120-4=126$

That is, the order in all exercises will be as follows:

Reminder: when an exercise includes operations that have the same precedence, that is, multiplication and division or addition and subtraction, we will solve the exercise from left to right.

Examples and Exercises with Solutions on Order of Operations with Parentheses

Exercise #1

$(7+2)\times(3+8)=$

Video Solution

Step-by-Step Solution

Simplify this expression paying attention to the order of operations. Whereby exponentiation precedes multiplication, division precedes addition and subtraction and that parentheses precede all of the above.

Therefore, let's first start by simplifying the expressions within the parentheses. After which we perform the multiplication between them:

$(7+2)\cdot(3+8)= \\ 9\cdot11=\\ 99$ Therefore, the correct answer is option B.

Answer

Exercise #2

$(85+5):10=$

Video Solution

Step-by-Step Solution

According to the order of operations rules, we must first solve the expression within the parentheses:

$85+5=90$

We should obtain the following expression:

$90:10=9$

Answer

Exercise #3

$8\times(5\times1)=$

Video Solution

Step-by-Step Solution

According to the order of operations, we first solve the expression in parentheses:

$5\times1=5$

Now we multiply:

$8\times5=40$

Answer

Exercise #4

Choose the exercise for the highest result

Video Solution

Step-by-Step Solution

Let's solve exercise A:

$8\times8=64$

Let's solve exercise B:

$10\times6=60$

Let's solve exercise C:

$12\times5=60$

Let's solve exercise D:

$15\times4=60$

Answer

$8\times(12-4)$

Exercise #5

$12:3(1+1)=$

Video Solution

Step-by-Step Solution

First, we perform the operation inside the parentheses:

$12:3(2)$

When there is no mathematical operation between parentheses and a number, we assume it is a multiplication.

Therefore, we can also write the exercise like this:

$12:3\times2$

Here we solve from left to right:

$12:3\times2=4\times2=8$

Answer

Check your understanding

Question 1

$$ (85+5):10= $$

Question 2

$$ (85+5):10= $$

Question 3

$8\times(5\times1)=$

Start practice