In previous articles, we have studied real numbers and the grouping of terms, as well as the order of mathematical operations with parentheses. In this article, we move forward and combine these topics in order to understand when and how we can eliminate parentheses in real numbers.
Elimination of Parentheses in Real Numbers
What does the elimination of parentheses in real numbers mean?
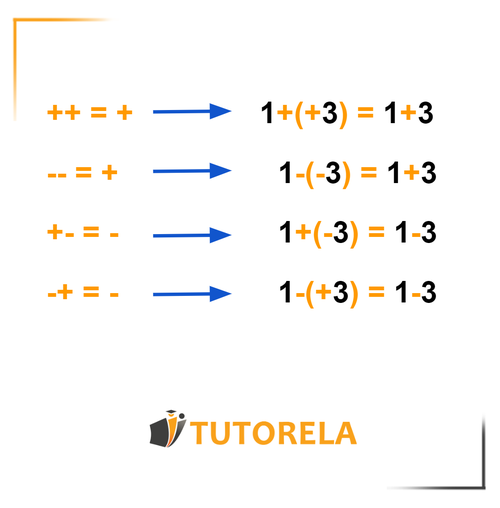
When we perform grouping of like terms ("addition and subtraction") with real numbers, we confine the real number within parentheses.
Parentheses can be removed but when eliminating them, the following rules must be remembered:
Test yourself on basic definitions!
What is the inverse number of \( 5 \)
The logic in this case is that the subtraction sign allows us to obtain the number opposite to the one given to us.
Consequently:
- "Minus minus six" is equal to "plus six", that is, "six".
- Similarly, "minus plus six" is equal to "minus six".
However, the plus sign does not indicate a modification in the number.
Therefore,
- "plus minus six" is equal to "minus six"
- and "plus plus six" is equal to "plus six", that is, "six".
Examples:
Let's look again at the three previously solved exercises, now we will write them without parentheses.
As we surely remember from the class on "real numbers", when a number has no sign, we understand it to be positive.
Therefore,
- in the first exercise, we can write "50" and "30" instead of "+50" and "+30".
- However, we cannot remove the plus sign in the third exercise: in "+4".
Remember: We can only omit the plus sign if the number is the first in the sequence.
When solving exercises with real numbers, in the first phase we will remove the parentheses according to mathematical rules.
Example:
Exercises on Eliminating Parentheses in Real Numbers
Exercise 1
Complete:
- __
- __
- __
- __
- __
- __
- -__
What is the additive inverse number of \( 87 \)
What is the inverse number of \( -7 \)
What is the inverse number of \( -0.25 \)
Exercise 2
Solve the following exercises, first of all, remove the parentheses:
Exercise 3
Assignment
Mark the correct answer
Solution
We solve the expressions inside the parentheses according to the order of arithmetic operations
We continue solving the expressions inside the parentheses accordingly.
Answer
What is the inverse number of \( 0.7 \)
What is the inverse number of \( -\frac{8}{7} \)
Before you is a series of numbers
\( \left(-30\right),\left(+55\right), \left(-5\right),\left(+8\right) \)
Arrange the numbers in ascending order from left to right
Exercise 4
Assignment
Solution
First, we solve the expressions within the parentheses according to the laws of addition and subtraction
We arrange the multiplication exercise we obtained to make it easier to solve.
We solve the exercise from left to right
Answer
Exercise 5
Assignment
Solution
First, we solve the expressions within the parentheses according to the laws of addition and subtraction
Note that we obtained a multiplication exercise with the number and we solve it first to simplify the calculation.
Answer
\( (+0.5)+(+\frac{1}{2})= \)
\( (+2.16)+(-4\frac{1}{16})= \)
\( (+\frac{18}{6})-(-\frac{1}{4})= \)
Exercise 6
Assignment
Solution
First, we solve the operations inside the parentheses according to the rules of addition and subtraction
We solve the operation from left to right
Answer
Exercise 7
Assignment
Solution
We multiply the first element inside the parentheses by the elements of the second parentheses
Then we multiply the second element inside the primary parentheses by the elements of the second parentheses
We solve all the multiplication exercises from left to right
Now we add from left to right
Answer
\( (+43)-(+15)= \)
\( (-\frac{2}{4})-(+3.5)= \)
\( (-3\frac{2}{6})+(-2.75)= \)
Examples with solutions for Elimination of Parentheses in Real Numbers
Exercise #1
What is the inverse number of
Video Solution
Step-by-Step Solution
To solve the problem of finding the opposite number of , we will use the concept of opposite numbers:
- Step 1: Identify the given number, which is .
- Step 2: Determine the opposite number by changing the sign. The opposite of is calculated as follows:
The opposite of a negative number is its positive counterpart. So, the opposite of is .
Therefore, the answer is .
Answer
Exercise #2
What is the additive inverse number of
Video Solution
Step-by-Step Solution
To solve this problem, we'll follow these steps:
- Step 1: Identify the given number
- Step 2: Apply the definition of an opposite number
- Step 3: Conclude with the opposite number
Now, let's work through each step with detailed explanations:
Step 1: We are given the number . This is a positive integer.
Step 2: The definition of an opposite number states that the opposite of any number is . Here, .
Step 3: Using the definition, the opposite number of is calculated as .
Therefore, the solution to the problem is .
Answer
Exercise #3
What is the inverse number of
Video Solution
Step-by-Step Solution
To solve this problem, we'll follow these steps:
- Step 1: Identify the given number.
- Step 2: Find its opposite by changing the sign.
Now, let's work through each step:
Step 1: The problem gives us the number .
Step 2: The opposite of a positive number is the same number with a negative sign.
Thus, the opposite of is .
Therefore, the opposite number of is .
Answer
Exercise #4
Before you is a series of numbers
Arrange the numbers in ascending order from left to right
Step-by-Step Solution
To arrange the numbers in ascending order, identify the numbers from the least to the greatest. Start by listing the numbers. Among them, is the smallest. Followed by , the next one is and the largest is . Therefore, in ascending order, the sequence is .
Answer
Exercise #5
What is the inverse number of
Video Solution
Step-by-Step Solution
To determine the opposite number of , we will simply change its sign, following these steps:
- Step 1: Identify the given number, which is .
- Step 2: Change the sign of to find its opposite. Since is positive, its opposite will be negative.
By changing the sign of , we get . Therefore, the opposite number of is .
In conclusion, the solution to the problem is .
Answer
More Questions
Basic Definitions
- The Order of Basic Operations: Addition, Subtraction, and Multiplication
- Addition and Subtraction of Real Numbers
- Multiplication and Division of Real Numbers
- Integer powering
- Positive and negative numbers and zero
- Real line or Numerical line
- The commutative property
- The Commutative Property of Addition
- The Commutative Property of Multiplication
- The Associative Property
- The Associative Property of Addition
- The Associative Property of Multiplication
- The Distributive Property
- The Distributive Property for Seventh Graders
- The Distributive Property of Division
- The Distributive Property in the Case of Multiplication
- The commutative properties of addition and multiplication, and the distributive property
- Exponents and Roots - Basic
- What is a square root?
- Square Root of a Negative Number
- Exponents and Exponent rules
- Basis of a power
- The exponent of a power
- Powers









