Parabola of the form y=(x-p)² - Examples, Exercises and Solutions

Family of Parabolas y=(x−p)2y=(x-p)^2

In this family, we have a slightly different quadratic function that shows us, very clearly, how the parabola shifts horizontally.
PP indicates the number of steps the parabola will move horizontally, to the right or to the left.
If PP is positive: (there is a minus sign in the equation) - The parabola will move PP steps to the right.
If PP is negative: (and, consequently, there will be a plus sign in the equation since minus by minus equals plus) - The parabola will move PP steps to the left.

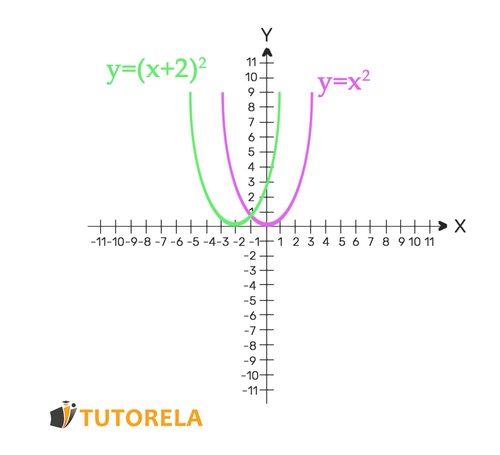
Let's see an example:
The function  Y=(X+2)2 Y=(X+2)^2

shifts two steps to the left.
Let's see it in an illustration:

1 - The function   Y=(X+2)^2

Detailed explanation

Suggested Topics to Practice in Advance

  1. The functions y=x²
  2. Families of Parabolas
  3. Family of Parabolas y=x²+c: Vertical Shift

Practice Parabola of the form y=(x-p)²

Question 1

What is the positive domain of the function below?

\( y=(x-2)^2 \)

Question 2

Find the intersection of the function

\( y=(x+4)^2 \)

With the Y

Question 3

Find the intersection of the function

\( y=(x-2)^2 \)

With the X

Question 4

Find the intersection of the function

\( y=(x-2)^2 \)

With the Y

Question 5

Find the intersection of the function

\( y=(x-6)^2 \)

With the Y

examples with solutions for parabola of the form y=(x-p)²

Exercise #1

What is the positive domain of the function below?

y=(x−2)2 y=(x-2)^2

Video Solution

Step-by-Step Solution

In the first step, we place 0 in place of Y:

0 = (x-2)²

 

We perform a square root:

0=x-2

x=2

And thus we reveal the point

(2, 0)

This is the vertex of the parabola.

 

Then we decompose the equation into standard form:

 

y=(x-2)²

y=x²-4x+2

Since the coefficient of x² is positive, we learn that the parabola is a minimum parabola (smiling).

If we plot the parabola, it seems that it is actually positive except for its vertex.

Therefore the domain of positivity is all X, except X≠2.

 

Answer

all x, x≠2 x\ne2

Exercise #2

Find the intersection of the function

y=(x+4)2 y=(x+4)^2

With the Y

Video Solution

Answer

(0,16) (0,16)

Exercise #3

Find the intersection of the function

y=(x−2)2 y=(x-2)^2

With the X

Video Solution

Answer

(2,0) (2,0)

Exercise #4

Find the intersection of the function

y=(x−2)2 y=(x-2)^2

With the Y

Video Solution

Answer

(0,4) (0,4)

Exercise #5

Find the intersection of the function

y=(x−6)2 y=(x-6)^2

With the Y

Video Solution

Answer

(0,36) (0,36)

Question 1

Find the positive area of the function

\( y=(x+6)^2 \)

Question 2

Find the positive area of the function
\( y=(x+5)^2 \)

Question 3

Find the negative area of the function

\( y=(x+2)^2 \)

Question 4

Find the negative area of the function

\( y+1=(x+3)^2 \)

Question 5

To work out the points of intersection with the X axis, you must substitute \( x=0 \).

examples with solutions for parabola of the form y=(x-p)²

Exercise #1

Find the positive area of the function

y=(x+6)2 y=(x+6)^2

Video Solution

Answer

x≠−6 x\ne-6

Exercise #2

Find the positive area of the function
y=(x+5)2 y=(x+5)^2

Video Solution

Answer

For each X x≠5 x\ne5

Exercise #3

Find the negative area of the function

y=(x+2)2 y=(x+2)^2

Video Solution

Answer

There is no

Exercise #4

Find the negative area of the function

y+1=(x+3)2 y+1=(x+3)^2

Video Solution

Answer

-4 < x < -2

Exercise #5

To work out the points of intersection with the X axis, you must substitute x=0 x=0 .

Video Solution

Answer

False

Question 1

To find the y axis intercept, you substitute \( x=0 \) into the equation and solve for y.

Question 2

To which chart does the function \( y=x^2 \) correspond?

1234

Question 3

One function

\( y=-x^2 \)

for the corresponding chart

-1-1-11234

Question 4

Find the ascending area of the function

\( y=(x-3)^2 \)

Question 5

Find the descending area of the function

\( y=(x-5)^2 \)

examples with solutions for parabola of the form y=(x-p)²

Exercise #1

To find the y axis intercept, you substitute x=0 x=0 into the equation and solve for y.

Video Solution

Answer

True

Exercise #2

To which chart does the function y=x2 y=x^2 correspond?

1234

Video Solution

Answer

2

Exercise #3

One function

y=−x2 y=-x^2

for the corresponding chart

-1-1-11234

Video Solution

Answer

2

Exercise #4

Find the ascending area of the function

y=(x−3)2 y=(x-3)^2

Video Solution

Answer

3 < x

Exercise #5

Find the descending area of the function

y=(x−5)2 y=(x-5)^2

Video Solution

Answer

x < 5

Topics learned in later sections

  1. Family of Parabolas y=(x-p)²+k (combination of horizontal and vertical shifts)