Families of Parabolas

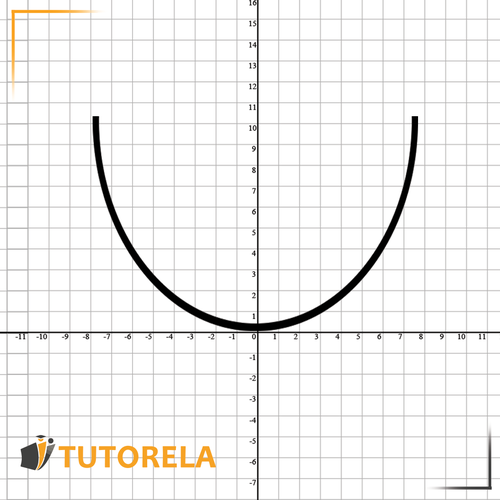
Meet the most basic quadratic function:
$y=X^2$
In this function:
$b=0~, c=0~, a=1$

*Relevant illustration in Word file*

The function is a smiling minimum function and its vertex is - $(0,0)$
The axis of symmetry of this function is $X=0$.
The increasing interval of the function – all the $X$ values where the function is increasing are: $X>0$
The decreasing interval of the function – all the $X$ values where the function is decreasing are: $X<0$
Positive interval: all $X$ except $0$ – you can see in the graph that the entire function is above the $X$ axis
Negative interval: none. The entire function is above the $X$ axis.
Let's continue to a similar function from the same family:
$y=-x^2$
In this function:
$a=-1 ,~b=0 ,~c=0$

*Relevant illustration in the Word file*

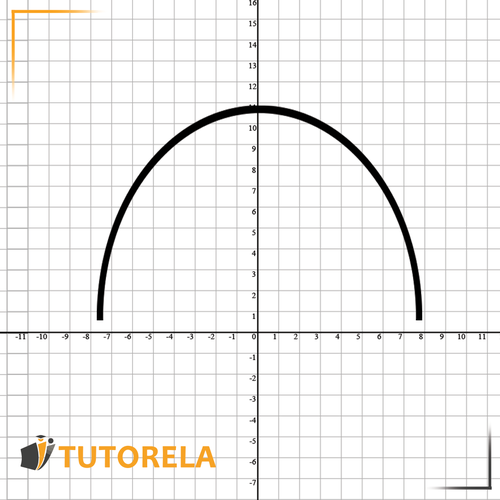
The function is a sad maximum function and its vertex is $(0,0)$
The axis of symmetry of this function is $X=0$.
Increasing interval: $X<0$
Decreasing interval: $X>0$
Positive interval: None. The entire function is below the $X$ axis.
Negative interval: All $X$ except $X=0$
Let's continue with another function from the same family:
$y=ax^2$
In this function:
$a=some~number,~b=0,~ c=0$ *Relevant illustration in Word file*

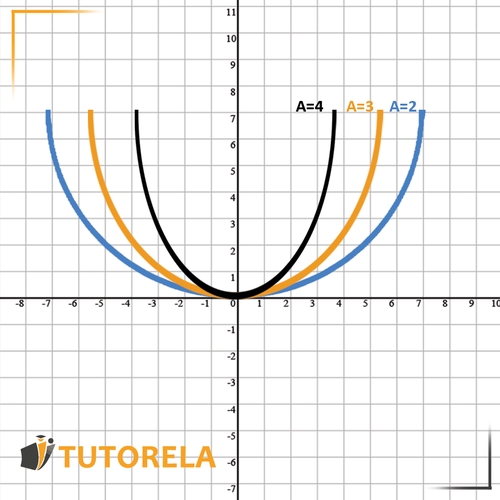
Its vertex is- $(0,0)$
The axis of symmetry of this function is $X=0$.

The larger $a$ is: the parabola will have a smaller opening – closer to its axis of symmetry.
The smaller $a$ is: the parabola will have a larger opening – farther from its axis of symmetry.

The function from this family has no horizontal or vertical shift because in every function from this family the vertex is $(0,0)$

Click here to practice and learn more about the function $y=X^2$

The family of parabolas $y=x^2+c$
The basic quadratic function – with the addition of $c$
In this function:
$c$ – represents the intersection point of the function with the $Y$ axis.
The meaning of $c$ is a vertical shift up or down of the function from the vertex $(0,0)$.
If $c$ is positive – the function will shift vertically up by the number of steps indicated by $c$.
If $c$ is negative – the function will shift vertically down by the number of steps indicated by $c$.

This function describes only vertical shifts up and down according to $c$
Let's see an example:
$y=4x^2+7$

In this function -
$C=7$
this means that the intersection point of the function with the $Y$ axis is $7$.
And actually – the function moves vertically $7$ steps up.
*Illustration in Word file*

Click here to practice and learn more about the function $y=X^2+c$

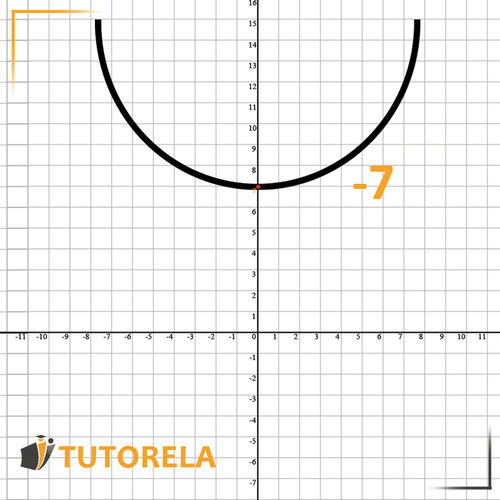
In this family, we are given a quadratic function that clearly shows us how the function moves horizontally – how many steps it needs to move right or left.
$P$ represents the number of steps the function will move horizontally – right or left.
If $P$ is positive – (there is a minus in the equation) – the function will move $P$ steps to the right.
If $P$ is negative – (and as a result, there is a plus in the equation because minus times minus equals plus) – the function will move $P$ steps to the left.
Let's see an example:
$Y=(X-6)^2$

This function moves from the vertex $(0,0)$,$6$ steps to the right
Let's see this in the figure: *relevant figure in the Word file*

Click here to practice and learn more about the function $y=(x-p)^2$

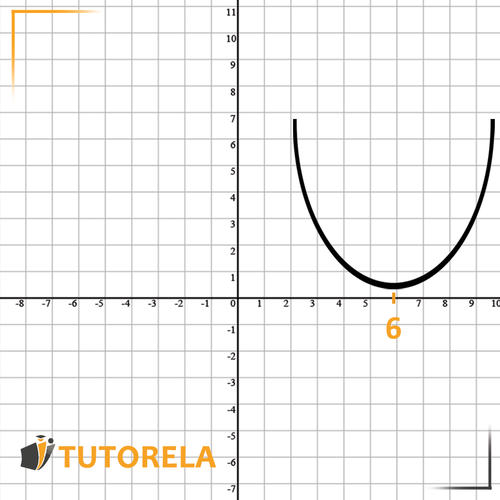
In this quadratic function, we can see a combination of horizontal and vertical shifts:
$K$: Determines the number of steps and the direction the function will move vertically – up or down.
$K$ positive – shift up, $K$ negative – shift down.
$P$: Determines the number of steps and the direction the function will move horizontally – right or left.

Let's look at an example of combining two translations together:
For example, in the function:
$y=(x+2)^2+5$

The changes will be:
According to $P=-2$: the parabola will move $2$ steps to the left.
According to $K=5$: the parabola will move $5$ steps up.

Let's see this in the illustration: *Relevant illustration in the Word file*

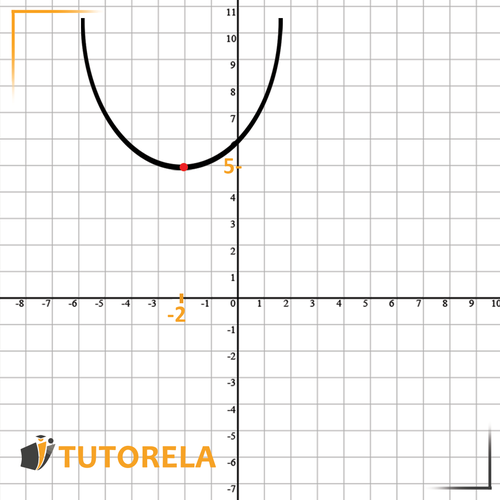
We can see that the vertex of the parabola is:
$(-2,5)$

Click here to practice and learn more about the function $y=(x-p)^2$