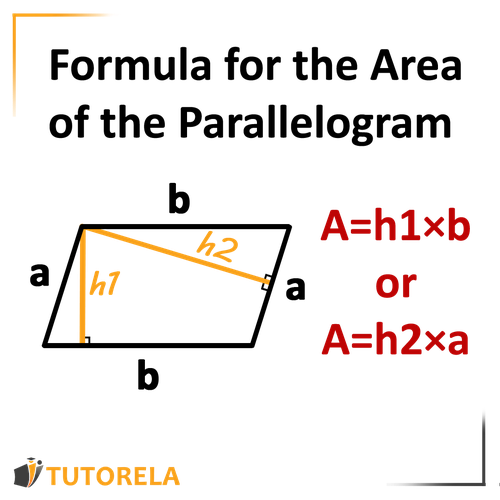
We can calculate the area of a parallelogram by multiplying one of its sides by its relative height.
To understand it better, we can use the following figure and the accompanying formula:
It can be seen that: and are the two heights corresponding to the bases and respectively.
Area of a Parallelogram