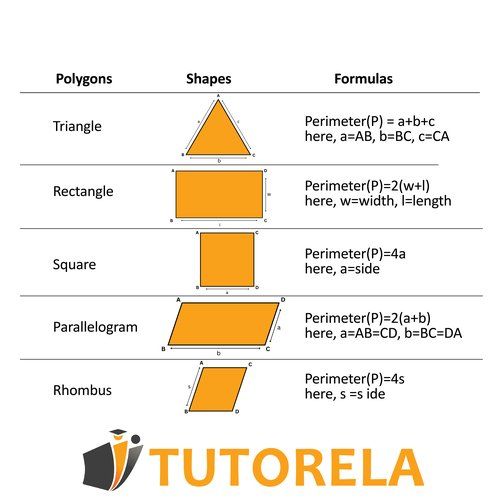
As long as we are dealing with a shape characterized by straight lines, the perimeter calculation will be performed by adding together all of the side lengths. This is a simple arithmetic operation that does not require any special skills. For example:
Triangle Perimeter Practice Problems - Step-by-Step Solutions
Master triangle perimeter calculations with practice problems covering equilateral, isosceles, and scalene triangles. Includes detailed solutions and formulas.
📚What You'll Master in Triangle Perimeter Practice
- Calculate perimeter by adding all three triangle sides together
- Solve equilateral triangle problems using the formula P = 3a
- Find missing sides in isosceles triangles using equal leg properties
- Apply triangle inequality theorem to verify valid triangle measurements
- Work with real-world triangle perimeter word problems and applications
- Master perimeter calculations for scalene triangles with different side lengths
Understanding Perimeter of a Triangle
Complete explanation with examples
How do we calculate the perimeter of polygons?
The perimeter of a shape with sides of 5, 9, 4, 6 and 7, will be 31. All you need to do is simply add up all of the sides.
Why can such a question be challenging? Owing to the fact that in tests, they don't want to examine you on arithmetic operations like addition, but rather on your proficiency in the properties of specific shapes. Therefore, you need to know the properties of polygons as they are.
Practice Perimeter of a Triangle
Test your knowledge with 53 quizzes
Calculate the perimeter of the given parallelogram:
Examples with solutions for Perimeter of a Triangle
Step-by-step solutions included
Exercise #1
Look at the rectangle below.
Side AB is 2 cm long and side BC has a length of 7 cm.
What is the perimeter of the rectangle?
Step-by-Step Solution
Given that in a rectangle every pair of opposite sides are equal to each other, we can state that:
Now we can add all the sides together and find the perimeter:
Answer:
18 cm
Video Solution
Exercise #2
Look at the rectangle below.
Side AB is 4.8 cm long and side AD has a length of 12 cm.
What is the perimeter of the rectangle?
Step-by-Step Solution
In the drawing, we have a rectangle, although it is not placed in its standard form and is slightly rotated,
but this does not affect that it is a rectangle, and it still has all the properties of a rectangle.
The perimeter of a rectangle is the sum of all its sides, that is, to find the perimeter of the rectangle we will have to add the lengths of all the sides.
We also know that in a rectangle the opposite sides are equal.
Therefore, we can use the existing sides to complete the missing lengths.
4.8+4.8+12+12 =
33.6 cm
Answer:
33.6 cm
Video Solution
Exercise #3
Look at the rectangle below.
Side DC has a length of 1.5 cm and side AD has a length of 9.5 cm.
What is the perimeter of the rectangle?
Step-by-Step Solution
Since in a rectangle every pair of opposite sides are equal to each other, we can state that:
Now we can add all the sides together and find the perimeter:
Answer:
22 cm
Video Solution
Exercise #4
Look at the triangle below:
What is the perimeter of the triangle?
Step-by-Step Solution
The perimeter of the triangle is equal to the sum of all sides together, therefore:
Answer:
24
Video Solution
Exercise #5
Given the triangle:
What is its perimeter?
Step-by-Step Solution
The perimeter of a triangle is equal to the sum of all its sides together:
Answer:
31
Video Solution
Frequently Asked Questions
How do you find the perimeter of a triangle?
+To find the perimeter of a triangle, add the lengths of all three sides together. The formula is P = a + b + c, where a, b, and c are the side lengths. This works for all triangle types including scalene, isosceles, and equilateral triangles.
What is the perimeter formula for an equilateral triangle?
+For an equilateral triangle, the perimeter formula is P = 3a, where 'a' is the length of one side. Since all three sides are equal in an equilateral triangle, you simply multiply one side length by 3.
How do you calculate perimeter of an isosceles triangle?
+For an isosceles triangle, use P = 2a + b, where 'a' is the length of the two equal legs and 'b' is the base. Since two sides are equal, you can multiply the leg length by 2 and add the base length.
What are the steps to solve triangle perimeter word problems?
+Follow these steps: 1) Identify the triangle type (scalene, isosceles, or equilateral), 2) List the known side lengths, 3) Use triangle properties to find missing sides, 4) Add all three sides together, 5) Include proper units in your final answer.
Can you find triangle perimeter if only two sides are given?
+You can only find the exact perimeter if you know the triangle type. For isosceles triangles, if you know one leg and the base, you can calculate the perimeter. For equilateral triangles, knowing one side gives you the perimeter. For scalene triangles, you need all three sides.
What is the difference between area and perimeter of a triangle?
+Perimeter is the total distance around the triangle's edges, calculated by adding all three sides (P = a + b + c). Area is the space inside the triangle, calculated using different formulas like A = ½ × base × height. Perimeter uses linear units while area uses square units.
How do you check if triangle side lengths are valid?
+Use the triangle inequality theorem: the sum of any two sides must be greater than the third side. Check all three combinations: a + b > c, a + c > b, and b + c > a. If all three conditions are true, the sides can form a valid triangle.
What are common mistakes when calculating triangle perimeter?
+Common mistakes include: forgetting to add all three sides, mixing up area and perimeter formulas, not using triangle properties to find missing sides, incorrect unit conversions, and not checking if the given sides can form a valid triangle using the triangle inequality theorem.