A polygon defines a geometric shape that is made up of sides. In other words, under the umbrella of polygons fall the following square, rectangle, parallelogram, trapezoid, and many more.
Area of Rectangle Practice Problems and Polygon Areas
Master rectangle area calculations and polygon area problems with step-by-step practice. Learn formulas, solve complex shapes, and build confidence in geometry.
📚What You'll Master in This Practice Session
- Calculate rectangle areas using the width × length formula
- Solve complex polygon area problems by dividing shapes into rectangles
- Apply the completion method to find areas of irregular polygons
- Master triangle, parallelogram, and trapezoid area calculations
- Combine multiple polygon areas to solve composite shape problems
- Use proper units and measurements in area calculations
Understanding Areas of Polygons for 7th Grade
Complete explanation with examples
Areas of Polygons
Polygon Definition
For example, a triangle has 3 sides, every quadrilateral has 4 sides, and so on.
We have already learned to calculate the areas of standard polygons. There are also non-standard polygons, for which there is no specific formula. However, their area of complex shapes can be calculated using two methods:
- We can divide the area of the required polygon into several areas of polygons that we are familiar with, calculate the areas separately, and then add them together to obtain the final area.
- We can try to "complete" the area of the required polygon into another polygon whose area we know how to calculate, and the proceed to subtract the area we added. This way, we can obtain the area of the original polygon.
Example
Let's demonstrate this using a simple exercise:
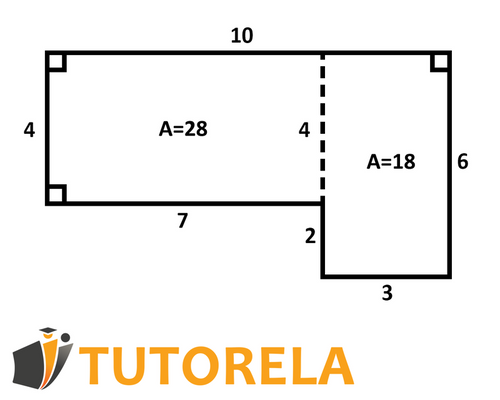
Here is a drawing of a polygon.
We need to calculate its area. From the start, we can see that this is not a standard polygon, so we will use the first method to calculate its area. We will divide the polygon as shown in the drawing, and we should obtain two rectangles.
According to the data shown in the drawing, in the rectangle on the right side we obtain the side lengths of 3 and 6, therefore the area of the rectangle will be 18 (multiplication of the two values). In the rectangle on the left side we obtain the side lengths of 4 and 7, therefore the area of the rectangle will be 28 (multiplication of the two values). Thus, the total area of the polygon will be the sum of the two areas we calculated separately, meaning, 18+28=46.
Practice Areas of Polygons for 7th Grade
Test your knowledge with 94 quizzes
ABCD is a rectangle.
Given in cm:
AB = 7
BC = 5
Calculate the area of the rectangle.
Examples with solutions for Areas of Polygons for 7th Grade
Step-by-step solutions included
Exercise #1
Calculate the area of the parallelogram according to the data in the diagram.
Step-by-Step Solution
We know that ABCD is a parallelogram. According to the properties of parallelograms, each pair of opposite sides are equal and parallel.
Therefore:
We will calculate the area of the parallelogram using the formula of side multiplied by the height drawn from that side, so the area of the parallelogram is equal to:
Answer:
70
Video Solution
Exercise #2
Calculate the area of the right triangle below:
Step-by-Step Solution
Due to the fact that AB is perpendicular to BC and forms a 90-degree angle,
it can be argued that AB is the height of the triangle.
Hence we can calculate the area as follows:
Answer:
24 cm²
Video Solution
Exercise #3
Calculate the area of the triangle ABC using the data in the figure.
Step-by-Step Solution
First, let's remember the formula for the area of a triangle:
(the side * the height that descends to the side) /2
In the question, we have three pieces of data, but one of them is redundant!
We only have one height, the line that forms a 90-degree angle - AD,
The side to which the height descends is CB,
Therefore, we can use them in our calculation:
Answer:
36 cm²
Video Solution
Exercise #4
The trapezoid ABCD is shown below.
AB = 2.5 cm
DC = 4 cm
Height (h) = 6 cm
Calculate the area of the trapezoid.
Step-by-Step Solution
First, let's remind ourselves of the formula for the area of a trapezoid:
We substitute the given values into the formula:
(2.5+4)*6 =
6.5*6=
39/2 =
19.5
Answer:
Video Solution
Exercise #5
The trapezoid ABCD is shown below.
Base AB = 6 cm
Base DC = 10 cm
Height (h) = 5 cm
Calculate the area of the trapezoid.
Step-by-Step Solution
First, we need to remind ourselves of how to work out the area of a trapezoid:
Now let's substitute the given data into the formula:
(10+6)*5 =
2
Let's start with the upper part of the equation:
16*5 = 80
80/2 = 40
Answer:
40 cm²
Video Solution
Frequently Asked Questions
What is the formula for calculating the area of a rectangle?
+The area of a rectangle is calculated using the formula: Area = width × length (or A = w × h). Simply multiply the rectangle's width by its length to find the total area in square units.
How do you find the area of complex polygons that aren't standard shapes?
+There are two main methods: 1) Divide the complex polygon into familiar shapes like rectangles and triangles, calculate each area separately, then add them together. 2) Complete the shape into a larger familiar polygon, then subtract the added area to get the original area.
What's the difference between area formulas for different polygons?
+Each polygon has its specific formula: Rectangle (width × length), Triangle (base × height ÷ 2), Parallelogram (base × height), and Trapezoid ((base₁ + base₂) × height ÷ 2). The key is identifying the shape correctly first.
How do you solve area problems with composite shapes made of rectangles?
+Step 1: Identify how to divide the composite shape into individual rectangles. Step 2: Find the dimensions of each rectangle from the given measurements. Step 3: Calculate each rectangle's area using length × width. Step 4: Add all individual areas together for the total area.
What units should I use when calculating polygon areas?
+Area is always measured in square units. If your measurements are in centimeters, the area will be in square centimeters (cm²). If in meters, then square meters (m²). Always include the proper square unit notation in your final answer.
Why do triangle and trapezoid area formulas include division by 2?
+These shapes can be thought of as half of a parallelogram or rectangle. A triangle is half of a parallelogram with the same base and height. A trapezoid's formula averages the two parallel bases, creating an equivalent rectangle, which is then divided by 2 to account for the slanted sides.
What are common mistakes students make when calculating rectangle areas?
+Common errors include: mixing up length and width (though it doesn't affect the answer), forgetting to include square units, adding instead of multiplying dimensions, and incorrectly reading measurements from diagrams. Always double-check your multiplication and units.
How can I check if my polygon area calculation is correct?
+Verification methods include: 1) Re-divide the shape differently and recalculate, 2) Estimate the area by comparing to known shapes, 3) Check that your answer makes sense given the dimensions, 4) Ensure all measurements use the same units, and 5) Verify your arithmetic by working backwards.