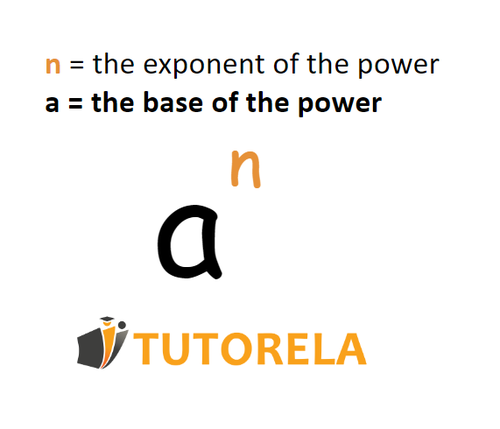
The exponent of a power - Examples, Exercises and Solutions

The exponent implies the number of times the base of the power must multiply itself.
In order for the base of the power to know how many times it should multiply itself, we must look at the exponent. The exponent denotes the power to which the base must be raised, that is, it determines how many times we will multiply the base of the power by itself.
How can they remember it?
It is called the exponent because (from the Latin exponentis) it makes visible or exposes how many times the base of the power will be multiplied.
In reality, it not only exposes but also determines.
How will we identify the exponent?
The exponent appears as a small number that is placed in the upper right corner of the base of the power.
It is not the main factor as the base is, therefore, its size is smaller and it appears discreetly to the right side and above it.

Detailed explanation

Practice The exponent of a power

Question 1

Find the value of n:

$6^n=6\cdot6\cdot6$ ?

Question 2

What is the answer to the following?

$$ 3^2-3^3 $$

Question 3

Sovle:

$$ 3^2+3^3 $$

Question 4

In the figure in front of you there are 3 squares

Write down the area of the shape in potential notation

Question 5

What is the missing exponent?

$-7^{\square}=-49$

examples with solutions for the exponent of a power

Exercise #1

Find the value of n:

$6^n=6\cdot6\cdot6$ ?

Video Solution

Step-by-Step Solution

We use the formula: $a\times a=a^2$

In the formula, we see that the power shows the number of terms that are multiplied, that is, two times

Since in the exercise we multiply 6 three times, it means that we have 3 terms.

Therefore, the power, which is n in this case, will be 3.

Answer

$n=3$

Exercise #2

What is the answer to the following?

$3^2-3^3$

Video Solution

Step-by-Step Solution

Remember that according to the order of operations, exponents come before multiplication and division, which come before addition and subtraction (and parentheses always before everything),

So first calculate the values of the terms in the power and then subtract between the results:

$3^2-3^3 =9-27=-18$ Therefore, the correct answer is option A.

Answer

$-18$

Exercise #3

Sovle:

$3^2+3^3$

Video Solution

Step-by-Step Solution

Remember that according to the order of operations, exponents precede multiplication and division, which precede addition and subtraction (and parentheses always precede everything).

So first calculate the values of the terms in the power and then subtract between the results:

$3^2+3^3 =9+27=36$ Therefore, the correct answer is option B.

Answer

Exercise #4

In the figure in front of you there are 3 squares

Write down the area of the shape in potential notation

Video Solution

Step-by-Step Solution

Using the formula for the area of a square whose side is b:

$S=b^2$ In the problem of the drawing, three squares whose sides have a length: 6, 3, and 4, units of length from left to right in the drawing respectively,

Therefore the areas are:

$S_1=3^2,\hspace{4pt}S_2=6^2,\hspace{4pt}S_3=4^2$ square units respectively,

Therefore, the total area of the shape, composed of the three squares, is as follows:

$S_{\text{total}}=S_1+S_2+S_3=3^2+6^2+4^2$ square units

Therefore, we recognize through the substitution property in addition that the correct answer is answer C.

Answer

$6^2+4^2+3^2$

Exercise #5

What is the missing exponent?

$-7^{\square}=-49$

Video Solution

Answer

Question 1

Choose the expression that is equal to the following:

$$ 2^7 $$

Question 2

Which of the following is equivalent to the expression below?

$$ $$ 10,000^1 $$

Question 3

$$ 6^2= $$

Question 4

$$ 11^2= $$

Question 5

Which of the following clauses is equal to 100?