Base of a Power Practice Problems & Exercises Online

To solve this problem, we'll focus on expressing the power $2^7$ as a series of multiplications.

• Step 1: Identify the given power expression $2^7$.
• Step 2: Convert $2^7$ into a product of repeated multiplication. This involves writing 2 multiplied by itself for a total of 7 times.
• Step 3: The expanded form of $2^7$ is $2 \times 2 \times 2 \times 2 \times 2 \times 2 \times 2$.

By comparing this expanded form with the provided choices, we see that the correct expression is:

$2\cdot2\cdot2\cdot2\cdot2\cdot2\cdot2$

Therefore, the solution to the problem is the expression that matches this expanded multiplication form, which is the choice $\text{1: } 2\cdot2\cdot2\cdot2\cdot2\cdot2\cdot2$.

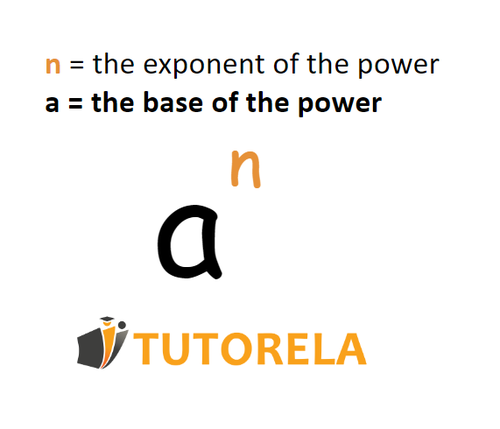
To solve this problem, we will apply the rule of exponents:

• Any number raised to the power of 1 remains unchanged. Therefore, by the identity property of exponents, $10,000^1 = 10,000$.

Given the choices:

• $10,000 \cdot 10,000$: This is $10,000^2$.
• $10,000 \cdot 1$: Simplifying this expression yields 10,000, which is equivalent to $10,000^1$.
• $10,000 + 10,000$: This results in 20,000, not equivalent to $10,000^1$.
• $10,000 - 10,000$: This results in 0, not equivalent to $10,000^1$.

Therefore, the correct choice is $10,000 \cdot 1$, which simplifies to 10,000, making it equivalent to $10,000^1$.

Thus, the expression $10,000^1$ is equivalent to:

$10,000 \cdot 1$

To solve this problem, we'll follow these steps:

• Step 1: Set up the multiplication as $11 \times 11$.
• Step 2: Compute the product using basic arithmetic.
• Step 3: Compare the result with the provided multiple-choice answers to identify the correct one.

Now, let's work through each step:
Step 1: We begin with the calculation $11 \times 11$.
Step 2: Perform the multiplication:

1. Multiply the units digits: $1 \times 1 = 1$.
2. Next, for the tens digits: $11 \times 10 = 110$.
3. Add the results: $110 + 1 = 111$. This doesn't seem right, so let's break it down further.

Let's examine a more structured multiplication method:

Multiply $11$ by $1$ (last digit of the second 11), we get 11.
Multiply $11$ by $10$ (tens place of the second 11), we get 110.

If we align correctly and add the partial products:

     11
+   110
------------
   121

Step 3: The correct multiplication yields the final result as $121$. Upon reviewing the provided choices, the correct answer is choice 4: $121$.

Therefore, the solution to the problem is $121$.

To solve this problem, we'll follow these steps:

• Step 1: Recognize that $6^2$ means $6 \times 6$.
• Step 2: Perform the multiplication of 6 by itself.

Now, let's work through each step:
Step 1: The expression $6^2$ indicates we need to multiply 6 by itself.
Step 2: Calculating $6 \times 6$ gives us 36.

Therefore, the value of $6^2$ is 36.

To determine which expression equals 100, we need to evaluate each option:

• Option 1: $5^2\cdot5$
  - Calculate $5^2 = 25$.
  - Then compute $25 \cdot 5 = 125$.
• Option 2: $4^2\cdot4$
  - Calculate $4^2 = 16$.
  - Then compute $16 \cdot 4 = 64$.
• Option 3: $25^4$
  - Calculate $(25^4)$, which simplified through breakdown is larger than 100 because $25^2 = 625$. Hence this 25 to the power of 4 will definitely be much larger than 100.
• Option 4: $5^2\cdot2^2$
  - Calculate $5^2 = 25$.
  - Calculate $2^2 = 4$.
  - Compute $25 \cdot 4 = 100$.

Therefore, the expression in Option 4, $5^2\cdot2^2$, equals 100. Thus, the correct choice is 4.

Thus, the clause that equals 100 is $5^2\cdot2^2$.