Basis of a power

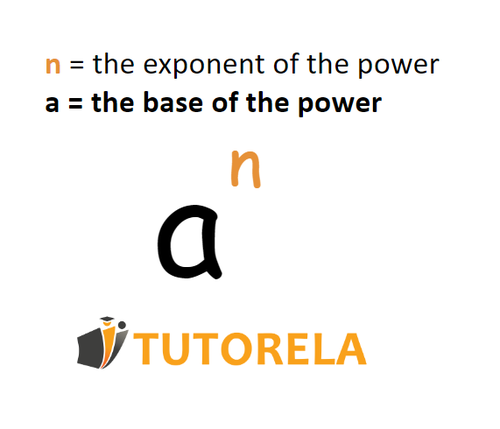
Points that are important to remember:

• When the base of the power is a positive number and the exponent is an even number the result will be positive.
• Even when the base of the power is a positive number and the exponent is an odd number, the result will also be positive.
• Even when the base of the power is a negative number and the exponent is an even number, the result will be positive.
• When the base of the power is a negative number and the exponent is odd, the result will be negative.

The base of the power is the number that is multiplied by itself as many times as indicated by the exponent.

How can you remember it?
It is called base because the power is raised on it: it is our base. If the power has no base, then there is no power.
How can we identify the base of the power?
The base of the power will appear as a number or algebraic expression. In its upper right corner we can see, in small, the exponent.
The base of the power has to stand out clearly since it is the base!
Let's see it in the following example:
$a^2$
What is the base of the power?
Of course a!
The base on which we raise the power is a.
In this example the exponent asks a, the base of the power, to multiply by itself twice.
That is:
$a\times a$
We can say that:
$a^2=a\times a$

If you liked this article, you may also be interested in the following articles

• The exponent of a power
• Powering Integers
• Multiplication of powers of equal base
• Division of powers of equal base
• Power of a Multiplication
• Power of a quotient
• Power of a power
• Power with zero exponent
• Powers of negative integer exponent
• Taking advantage of all the properties of powers or exponent laws
• Powering integers

On the Tutorela blog you will find a variety of articles about mathematics.

Prompt

What is the value we will place to solve the following equation?

$7^{\square}=49$

Solution

To answer this question it is possible to answer in two ways:

One way is replacement:

We place power of $2$ and it seems that we have arrived at the correct result, ie:

$7²=49$

Another way is by using the root

$\sqrt{49}=7$

That is

$7²=49$

Answer:

$2$

Query

What is the result of the following power?

$(\frac{2}{3})^3$

To solve this question we must first understand the meaning of the exercise.

$(\frac{2}{3})\cdot(\frac{2}{3})\cdot(\frac{2}{3})$

$\frac{2}{3}\cdot\frac{2}{3}\cdot\frac{2}{3}$

Now everything is simpler... Correct?

$2\cdot2\cdot2=8$

$3\cdot3\cdot3=27$

We obtain: $\frac{8}{27}$

Answer

$\frac{8}{27}$

Consigna

$a\cdot b\cdot a\cdot b\cdot a^2$

Solution:

If we break down the exercise we see that it is divided into $2$ coefficients of $a$ and coefficients of $b$

Let's start with the coefficient of $a$

What do we have?

We have $a\cdot a\cdot a²$

That is, we can write this like this:

$a\cdot a\cdot a\cdot a$

This means we can write it like this:

$a^4$

Let's move on to the coefficient $b$.

$b\cdot b=b²$

We add the two together and it turns out that:

$a^4\cdot b^2$

Answer:

$a^4\cdot b^2$

Assignment

Solve the exercise:

$\left(a^5\right)^7=$

Solution

We will use the formula

$(a^m)^n=a^{m\times n}$

We multiply the powers together and solve accordingly.

$a^{5\times7}=a^{35}$

Answer

$a^{35}$

Consigna

$(y\times7\times3)^4=$

Solution

We will use the formula

$(a\times b\times c)^m=a^m\times b^m\times c^m$

We solve accordingly

$(y\times7\times3)^4=y^4\times7^4\times3^4$

Answer

$y^4\times7^4\times3^4$

In order to read a power, there are special cases such as the power $2$ and $3$.

$a^2$ can be read as: "$a$ to the second power", "$a$ squared" or "$a$ to the power two."

$a^3$ can be read as: "$a$ to the third power", "$a$ cubed".

The others we can read as:

$a^x$ "$a$ raised to the power $x$"

$a^4$,$a$ to the fourth power", " to the fourth power", " to the fifth power", " to the fifth power".

$a^5$,$a$ to the fifth power".

$a^6$: "$a$ to the sixth power" : " to the sixth power".

In this example the base is $3$ and the power is the $2$

When we have a negative number and we raise it to a power we can have the following cases:

$\left(-x\right)^{\text{par}}=+$

$\left(-x\right)^{impar}=-$

Let's look at the following examples:

Calculate the following power

$\left(-2\right)^3$

We can observe that it is a negative number raised to an odd power, therefore the result will be negative, since by the law of signs it is as follows:

$\left(-2\right)^3=\left(-2\right)\left(-2\right)\left(-2\right)=\left(4\right)\left(-2\right)=-8$

Answer

$-8$

Calculate the following power

$\left(-4\right)^4=$

In this example we observe that the power is even, therefore the result will be positive by sign laws, remaining as follows:

$\left(-4\right)^4=\left(-4\right)\left(-4\right)\left(-4\right)\left(-4\right)=\left(16\right)\left(-4\right)\left(-4\right)$

$\left(16\right)\left(-4\right)\left(-4\right)=\left(-64\right)\left(-4\right)=256$

Answer

$256$