Converting Decimals to Mixed Numbers Practice Problems

Master converting decimal fractions to mixed numbers and simple fractions with step-by-step practice problems. Learn tenths, hundredths, and thousandths conversion techniques.

📚Master Decimal to Mixed Number Conversions
  • Convert decimals like 9.56 to mixed numbers using place value understanding
  • Identify tenths, hundredths, and thousandths in decimal fractions correctly
  • Practice reading decimal fractions aloud to determine proper denominators
  • Simplify converted fractions to lowest terms when possible
  • Apply conversion skills to real-world decimal problems
  • Build confidence with step-by-step conversion methods

Understanding Converting Decimal Fractions to Simple Fractions and Mixed Numbers

Complete explanation with examples

Converting a decimal to a mixed number

To convert a decimal fraction to a mixed fraction,
we ask ourselves how to read the decimal fraction or in other words, what the last digit represents –
if we use the word tenths – we place 10 in the denominator
if we use the word hundredths – we place 100 in the denominator
if we use the word thousandths – we place 1000 in the denominator

The number itself – everything that appears after the decimal point, we place in the numerator.
The whole number in the decimal fraction, we add to the mixed fraction as the whole number in the mixed fraction.

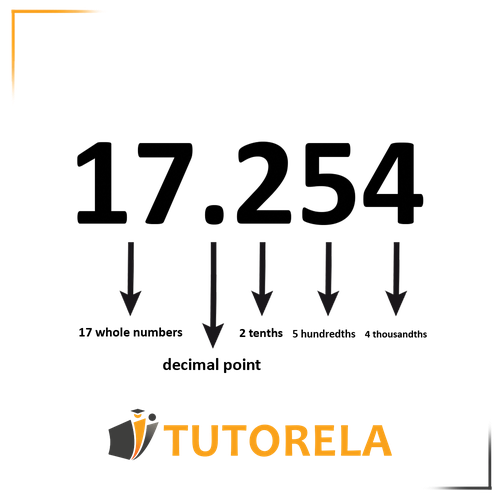
Converting a Decimal Fraction to a Mixed Number

Detailed explanation

Practice Converting Decimal Fractions to Simple Fractions and Mixed Numbers

Test your knowledge with 58 quizzes

Write the following fraction as a decimal:

\( \frac{66}{100}= \)

Examples with solutions for Converting Decimal Fractions to Simple Fractions and Mixed Numbers

Step-by-step solutions included
Exercise #1

Write the following fraction as a decimal:

2100= \frac{2}{100}=

Step-by-Step Solution

Let's write the simple fraction as a decimal fraction

2.0 2.0

Since the fraction divides by 100, we move the decimal point once to the left and get:

.020 .020

We'll add the zero before the decimal point and get:

0.020=0.02 0.020=0.02

Answer:

0.02

Video Solution
Exercise #2

Write the following fraction as a decimal:

3100= \frac{3}{100}=

Step-by-Step Solution

Let's write the simple fraction as a decimal fraction

3.0 3.0

Since the fraction divides by 100, we move the decimal point once to the left and get:

.030 .030

We'll add the zero before the decimal point and get:

0.030=0.03 0.030=0.03

Answer:

0.03

Video Solution
Exercise #3

Write the following fraction as a decimal:

33100= \frac{33}{100}=

Step-by-Step Solution

Let's write the simple fraction as a decimal fraction

33.0 33.0

Since the fraction divides by 100, we'll move the decimal point once to the left and get:

.330 .330

We'll add the zero before the decimal point and get:

0.330=0.33 0.330=0.33

Answer:

0.33

Video Solution
Exercise #4

Write the following fraction as a decimal:

14100= \frac{14}{100}=

Step-by-Step Solution

Let's write the simple fraction as a decimal fraction

14.0 14.0

Since the fraction divides by 100, we'll move the decimal point once to the left and get:

.140 .140

We'll add the zero before the decimal point and get:

0.140=0.14 0.140=0.14

Answer:

0.14

Video Solution
Exercise #5

Write the following fraction as a decimal:

4100= \frac{4}{100}=

Step-by-Step Solution

Let's write the simple fraction as a decimal fraction

4.0 4.0

Since the fraction divides by 100, we move the decimal point once to the left and get:

.040 .040

We'll add the zero before the decimal point and get:

0.040=0.04 0.040=0.04

Answer:

0.04

Video Solution

Frequently Asked Questions

Everything you need to know about Converting Decimal Fractions to Simple Fractions and Mixed Numbers

How do you convert a decimal to a mixed number?

+
To convert a decimal to a mixed number, identify what the last digit represents (tenths, hundredths, or thousandths), use that as your denominator, place all digits after the decimal point in the numerator, and keep the whole number part unchanged.

What denominator do I use for tenths, hundredths, and thousandths?

+
Use these denominators: tenths = 10, hundredths = 100, thousandths = 1000. The denominator matches the place value name - tenths comes from 10, hundredths from 100, and thousandths from 1000.

How do you read decimal fractions correctly?

+
Read the whole number first, then identify the fractional part by the last digit's place value. For example, 9.56 is read as '9 whole and 56 hundredths' because the 6 is in the hundredths place.

Can I simplify fractions after converting from decimals?

+
Yes, you should simplify converted fractions when possible. For example, 1.65 becomes 1 65/100, which simplifies to 1 13/20 by dividing both numerator and denominator by 5.

What's the difference between 7.2 and 7.200 when converting?

+
Both equal the same value but convert differently: 7.2 = 7 2/10 (tenths), while 7.200 = 7 200/1000 (thousandths). You can simplify 7 200/1000 to 7 2/10 since they're equivalent.

Why do trailing zeros matter in decimal conversion?

+
Trailing zeros determine the place value of the last significant digit. 4.2 has tenths as the last place (denominator 10), while 4.20 has hundredths as the last place (denominator 100), even though both equal the same value.

What are common mistakes when converting decimals to mixed numbers?

+
Common mistakes include: using wrong denominators, forgetting the whole number part, misreading place values, and not simplifying final answers. Always identify the last digit's place value first.

How do I practice converting decimals to mixed numbers effectively?

+
Start by reading decimals aloud to identify place values, practice with simple examples like 3.4 or 2.75, then progress to more complex decimals. Always check your work by converting back to decimal form.

More Converting Decimal Fractions to Simple Fractions and Mixed Numbers Questions

Click on any question to see the complete solution with step-by-step explanations

Converting Decimal Fractions to Simple Fractions and Mixed Numbers

Solve: 1/2 + 0.5 - 0 Using Mixed Number Formats Solve Mixed Number Equation: Converting 2 4/200 to Decimal Form Convert Mixed Number: Simplifying 2 31/100 to Decimal Form Complete the Expression: Finding Values Equal to 2.4 Convert Fraction to Decimal: Finding the Decimal Form of 1/100

Continue Your Math Journey

Master Converting Decimal Fractions to Simple Fractions and Mixed Numbers first, then advance to these related topics that build on your fraction skills

Suggested Topics to Practice in Advance

What is a Decimal Number?Decimal fraction remainderRemaindersDecimal FractionsReducing and Expanding Decimal Numbers

Topics Learned in Later Sections

Converting a simple fraction to decimal - how to calculate?Addition and Subtraction of Decimal NumbersComparison of Decimal NumbersConverting Decimals to Fractions

Practice by Question Type

Choose your preferred learning style and practice format for fraction problems
Comparison to simple fractions Conversion from non-round denominator Conversion - greater than 1 Convert a decimal to a fraction with 100 as its denominator Convert a fraction with a denominator greater than 100 to a decimal Convert a fraction with a denominator of 10 to a decimal Convert a fraction with a denonimator of 100 to a decimal Converting to a fraction in its simplest form Find the missing number From a decimal to a denominator of 10 Graphical representation Simple conversion to denominator 10, 100, 1000 Solving the problem