Converting Decimals to Fractions Practice Problems

Master decimal to fraction conversion with step-by-step practice problems. Learn to convert tenths, hundredths, thousandths to simple fractions and mixed numbers.

📚Master Decimal to Fraction Conversion with Targeted Practice

Convert decimal numbers like 0.3, 0.75, and 0.200 to simple fractions
Transform decimals with whole numbers into proper mixed number format
Practice reading decimal places to determine correct denominators (10, 100, 1000)
Simplify converted fractions by finding common factors and reducing
Apply the tenths, hundredths, thousandths rule for accurate conversion
Solve real-world problems involving decimal to fraction transformation

Understanding Converting Decimals to Fractions

Complete explanation with examples

To convert a decimal number to a simple fraction
we will ask ourselves how the decimal number
is read. If we use the word tenths, we will place $10$ in the denominator
If we use the word hundredths, we will place $100$ in the denominator
If we use the word thousandths, we will place $1000$ in the denominator.

The number itself will be placed in the numerator.
*If the integer figure differs from $0$ , we will note it next to the simple fraction.

Chart illustrating the conversion of decimal numbers to fractions, categorized by one-digit, two-digit, and three-digit decimals, including examples like 0.7 = 7/10 and 0.562 = 562/100.

Detailed explanation

Practice Converting Decimals to Fractions

Test your knowledge with 58 quizzes

Write the following fraction as a decimal:

$\frac{66}{100}=$

Examples with solutions for Converting Decimals to Fractions

Step-by-step solutions included

Exercise #1

Write the following fraction as a decimal:

$\frac{2}{100}=$

Step-by-Step Solution

Let's write the simple fraction as a decimal fraction

$2.0$

Since the fraction divides by 100, we move the decimal point once to the left and get:

$.020$

We'll add the zero before the decimal point and get:

$0.020=0.02$

Answer:

0.02

Video Solution

Exercise #2

Write the following fraction as a decimal:

$\frac{3}{100}=$

Step-by-Step Solution

Let's write the simple fraction as a decimal fraction

$3.0$

Since the fraction divides by 100, we move the decimal point once to the left and get:

$.030$

We'll add the zero before the decimal point and get:

$0.030=0.03$

Answer:

0.03

Video Solution

Exercise #3

Write the following fraction as a decimal:

$\frac{33}{100}=$

Step-by-Step Solution

Let's write the simple fraction as a decimal fraction

$33.0$

Since the fraction divides by 100, we'll move the decimal point once to the left and get:

$.330$

We'll add the zero before the decimal point and get:

$0.330=0.33$

Answer:

0.33

Video Solution

Exercise #4

Write the following fraction as a decimal:

$\frac{14}{100}=$

Step-by-Step Solution

Let's write the simple fraction as a decimal fraction

$14.0$

Since the fraction divides by 100, we'll move the decimal point once to the left and get:

$.140$

We'll add the zero before the decimal point and get:

$0.140=0.14$

Answer:

0.14

Video Solution

Exercise #5

Write the following fraction as a decimal:

$\frac{4}{100}=$

Step-by-Step Solution

Let's write the simple fraction as a decimal fraction

$4.0$

Since the fraction divides by 100, we move the decimal point once to the left and get:

$.040$

We'll add the zero before the decimal point and get:

$0.040=0.04$

Answer:

0.04

Video Solution

Frequently Asked Questions

Everything you need to know about Converting Decimals to Fractions

How do you convert a decimal to a fraction step by step?

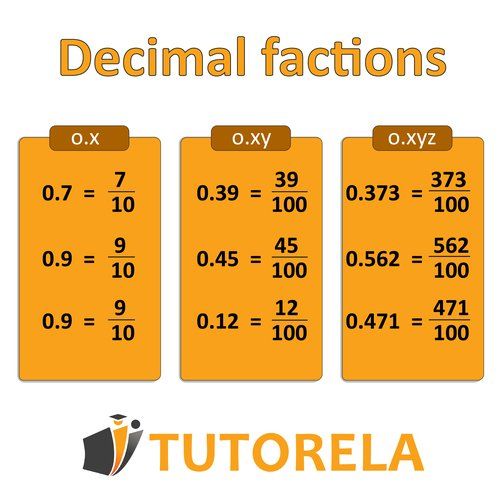
First, read the decimal aloud to identify the place value (tenths, hundredths, thousandths). Then place the decimal digits in the numerator and the corresponding place value (10, 100, 1000) in the denominator. Finally, simplify the fraction if possible by dividing both parts by their greatest common factor.

What denominator do I use when converting 0.75 to a fraction?

Use 100 as the denominator because 0.75 is read as '75 hundredths.' The last digit (5) is in the hundredths place, so you get 75/100, which simplifies to 3/4.

How do you convert decimals with whole numbers to mixed numbers?

Keep the whole number part separate and convert only the decimal portion to a fraction. For example, 4.25 becomes 4 and 25/100, written as 4 25/100 or simplified to 4 1/4.

Why does 0.200 equal 200/1000 instead of 2/10?

The conversion depends on the last significant digit's place value. Since 0.200 has its last digit in the thousandths place, you write it as 200/1000. However, both 200/1000 and 2/10 are equivalent when simplified.

What's the easiest way to remember decimal place values for fractions?

Count the decimal places: 1 decimal place = tenths (/10), 2 decimal places = hundredths (/100), 3 decimal places = thousandths (/1000). The number of zeros in the denominator matches the number of decimal places.

Do I always need to simplify fractions after converting from decimals?

While not always required, simplifying fractions is recommended for the clearest answer. For example, 75/100 should be reduced to 3/4, and 200/1000 should be simplified to 1/5 for easier understanding and use.

How do you convert repeating decimals to fractions?

Repeating decimals require algebraic methods beyond basic place value conversion. For terminating decimals covered in this topic, use the place value method: identify the rightmost digit's place value and use it as your denominator.

What common mistakes should I avoid when converting decimals to fractions?

Common errors include: using the wrong denominator (not matching decimal places), forgetting to simplify the final fraction, misreading the decimal place values, and incorrectly handling whole number parts in mixed decimals.

Continue Your Math Journey

Master Converting Decimals to Fractions first, then advance to these related topics that build on your fraction skills

Topics Learned in Later Sections

Converting a Decimal Fraction to a Mixed Number Converting a simple fraction to decimal - how to calculate?Addition and Subtraction of Decimal Numbers Comparison of Decimal Numbers

Practice by Question Type

Choose your preferred learning style and practice format for fraction problems

Comparison to simple fractions Conversion from non-round denominator Conversion - greater than 1 Convert a decimal to a fraction with 100 as its denominator Convert a fraction with a denominator greater than 100 to a decimal Convert a fraction with a denominator of 10 to a decimal Convert a fraction with a denonimator of 100 to a decimal Converting to a fraction in its simplest form Find the missing number From a decimal to a denominator of 10 Graphical representation Simple conversion to denominator 10, 100, 1000 Solving the problem

Converting Decimals to Fractions Practice Problems

Understanding Converting Decimals to Fractions

Practice Converting Decimals to Fractions

Examples with solutions for Converting Decimals to Fractions

Frequently Asked Questions

How do you convert a decimal to a fraction step by step?

What denominator do I use when converting 0.75 to a fraction?

How do you convert decimals with whole numbers to mixed numbers?

Why does 0.200 equal 200/1000 instead of 2/10?

What's the easiest way to remember decimal place values for fractions?

Do I always need to simplify fractions after converting from decimals?

How do you convert repeating decimals to fractions?

What common mistakes should I avoid when converting decimals to fractions?

More Converting Decimals to Fractions Questions

Converting Decimal Fractions to Simple Fractions and Mixed Numbers

Continue Your Math Journey

Suggested Topics to Practice in Advance

Topics Learned in Later Sections

Practice by Question Type