Decimal Fractions

Amplification of Decimal Numbers
We will add the digit $0$ to the end of the decimal number (to the right), and thus, the value of the decimal number will not change.
Reduction of Decimal Numbers
If the digit in the far-right position is $0$, we will remove it and the value of the decimal number will not change.

You can read more in the assigned extended article

We will solve these operations vertically keeping in mind the following rules:
• We will take into account the rules of addition and subtraction of integers.
• Decimal points must always be positioned one below the other.
• We will write the numbers in an orderly manner - both to the right of the decimal point and to its left. (tenths below tenths, hundredths below hundredths, and so on)

You can read more in the assigned extended article

First step:
We will control the whole parts - the decimal number with the largest whole number will be the largest of them.
Second step:
In case the whole numbers are identical we will check the digits that appear after the point.
We will go digit by digit (starting with the tenths, then hundredths, and so on)
If they continue to be equal, we proceed with the comparison of the following ones.
If they are different, we can determine which number is the largest.

You can read more in the assigned extended article

Let's see how to read the fraction
If we use the word tenths, we will place $10$ in the denominator
If we use the word hundredths, we will place $100$ in the denominator
If we use the word thousandths, we will place $1000$ in the denominator.

We will place the number itself in the numerator.
*If the integer figure differs from $0$, we will note it next to the simple fraction.

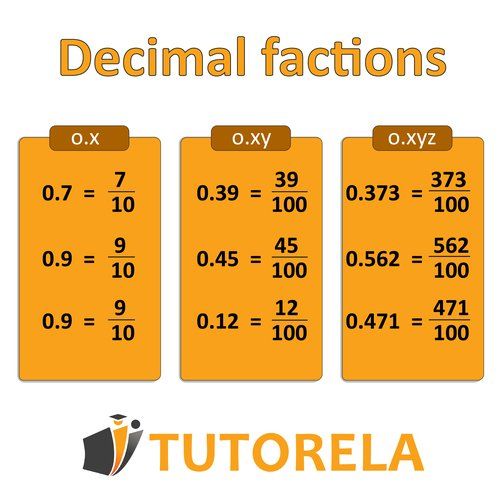
You can read more in the assigned extended article

First, we will convert the decimal number to a fraction according to the rules.
Then, we will convert the simple fraction to a mixed number using the following method:
We will calculate how many whole times the numerator fits into the denominator - this will be the whole number.
What remains, we will write in the numerator, and the denominator will remain unchanged (does not change).

You can read more in the assigned extended article

In multiplications: we will slide the decimal point to the right as many steps as the number has zeros.
In divisions: we will slide the decimal point to the left as many steps as the number has zeros.

You can read more in the assigned extended article

We will solve using the vertical multiplication method according to the following steps:
*We will write the numbers neatly one under the other, including the decimal points, one under the other, tenths under tenths, hundredths under hundredths, etc.
*We will solve the exercise, for now, we will not pay attention to the decimal point and will only act according to the rules of vertical multiplication.
*We will review each number in the exercise and count how many digits there are after the decimal point.
We will add up the total number of digits that are after the decimal point (taking into account both numbers) and that will be the number of digits that will be after the decimal point in the final answer.

You can read more in the assigned extended article

We will proceed in the following order:
First step -> We will make the decimal point in the dividend (the number we want to divide) disappear, moving it to the right the necessary number of places until it is completely gone.
Second step -> In the divisor (the second number in the operation, that is, the number by which it is divided) we will move the decimal point to the right the same number of places that we moved in the first number (even if this number of steps is not enough to make it disappear)
Third step -> We will solve the "new" exercise (with the "new" numbers).

You can read more in the assigned extended article

A repeating decimal is a number with a fractional part that, after the decimal point, the digits repeat infinitely, in a periodic manner.
To learn how to convert a fraction to a repeating decimal, consult the complete article on this topic.

You can read more in the assigned extended article

To equalize decimal measures, we will proceed as follows:
We will identify the largest unit of measure between the two numbers, convert the number with the smaller unit of measure to the larger unit of measure, and compare both numbers that now have the same unit of measure.

You can read more in the assigned extended article

Between any pair of numbers, there is an infinite number of other numbers.

You can read more in the assigned extended article