Discrete graph

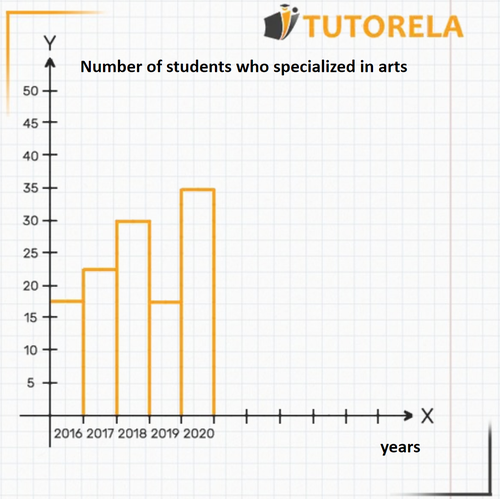
• In this graph, the years are placed on the $X$ axis, while on the $Y$ axis are the number of students who specialized in arts at a particular school.
• Each column is separate and does not form a sequence of columns before or after it.
• Through this bar diagram, it is possible to get an impression of the changes that have taken place over the years in the number of students in the arts branch, but there is no numerical sequence between these values.

If you are interested in more information about "graphs" you can find detailed information in the following articles:

Data Collection and Organization - Statistical Research

Reading Information from Graphs

Graph

Continuous Graph

Graphical Representation of a Function

In the blog of Tutorela you will find a variety of articles with interesting explanations about mathematics

Sometimes graphs may seem complicated, but if we understand how they work, we will see that they are actually very simple. A graph is just a way to show a lot of information at once.

We have several basic types of graphs. In this article, we will learn about discrete graphs. To understand how they work, we will start with an example. In the example shown below, you can see a graph that represents the number of students who took Art in each academic year.

Every graph is composed of two axes: the $X$ axis and the $Y$ axis. The $X$ axis is the horizontal one (we can imagine it as the floor of the graph). In this graph, it indicates the years, as explicitly stated. The $Y$ axis is the vertical one (we can imagine it as the wall of the graph). In this graph, it indicates the number of students studying art, as written next to it, in the title: $5, 10, 15,$ etc. up to $50$.

In this article, we will learn to analyze the graph of the function.

Every graph is composed of two axes: the $X$ axis and the $Y$ axis. The $X$ axis is the horizontal one (we can imagine it as the floor of the graph). In a discrete graph like ours, the $X$ axis will represent different categories. Let's look at the example we have. Try to identify the $X$ axis, it is marked with that letter.

In this case, the $X$ axis indicates the category Years, as described, to its right, in the title. We can see the years written on the graph below each column: $2016, 2017$ and so on.

The $Y$ axis is the vertical one (we can imagine it as the wall of the graph). In this graph, it indicates the number of students studying art, as written next to it, in the title: $5, 10, 15,$ etc. up to $50$.

Through this graph, we will interpret how many students studied Art each year. This information is represented in the columns.

For example, let's look at the $X$ axis in the year $2018$. We see that over the year $2018$ there is an orange column that rises up to the number $30$ on the $Y$ axis. This means that in the year $2018$ exactly $30$ students studied Art.

Another example, let's look at the $X$ axis in the year $2020$. The column over $2020$ rises exactly to the number 35 on the $Y$ axis. That is, in the year $2020$ exactly $35$ students studied Art.

Now, try it yourself, let's see if you can find out how many students took Art in the year $2017$. Identify the requested year on the $X$ axis. Now you will notice that the column rising from the year $2017$ does not reach a clearly marked point on the $Y$ axis. However, we can see that the graph reaches approximately a midpoint between $20$ and $25$. So, it is probably about $22$ or $23$ students (since it cannot be $22.5$ students, it would be impossible to think of half a student).

Although the exact answer is not entirely clear, it is enough for us. Knowing that it is about $22$ or $23$ students is sufficient. This is the information we can deduce from this graph as it is. If the graph of the function were more detailed, we could deduce exactly how many students studied Art in the year $2017$.

The reason for the name used for this type of graph "discrete graph" is because each category acts "at its own discretion" and without relation to the others. There is no continuity between the categories, each column is independent and unrelated to the adjacent ones. Next, we will see a graph of another type, a continuous graph.