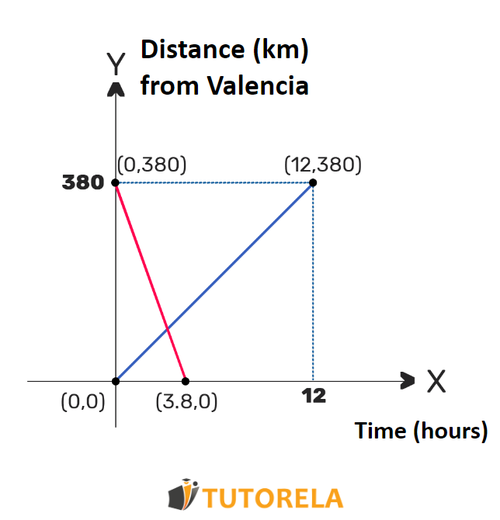
A linear function describes the relationship between X and Y. Therefore, we can represent all sorts of different phenomena in life with the help of the linear function. The representation of phenomena with the help of linear functions is expressed in mathematics in word problems, using graphs of the functions. Thus, we can find the various relationships between the functions.
Representing phenomena using linear functions actually allows us to simplify many word questions using a simple linear graph. From the graph, we can very easily calculate the slope, which is actually the rate of change and even many other parameters.
Example of representing phenomena using linear functions
At 10 in the morning, truck A left the factory in Valencia for the factory in Madrid, a distance of 380 km. At the same time, truck B left the factory in Madrid for the factory in Valencia.
The two trucks were supposed to meet somewhere along the way. The figure in front of you shows graphs that describe the position of the drivers at any time during the journey.
What does each marked point on the graph mean?
Solution: Let's first look at the points on the blue graph: We can associate the blue graph with truck A since we see it started from the point (0,0). Truck A departed from a point which is the distance from Valencia was 0 km, meaning it left from Valencia. Therefore, the point (0,0) is the starting point of truck A. The second point on the blue graph: ( 12,380) represents the arrival point of truck A in Madrid. After 12 hours and after 380 km.
Now let's look at the points on the purple graph: (3.8,0) this point represents truck B and shows us that after 3.8 hours, the truck arrived in Valencia: its distance from Valencia was 0 km. (0,380 ): represents truck B and shows us its starting point where it had not yet begun to travel and its distance to Valencia was 380 km.
Join Over 30,000 Students Excelling in Math!
Endless Practice, Expert Guidance - Elevate Your Math Skills Today
Test your knowledge
Question 1
The graph below depicts the price of apples relative to the quantity.
When and at what distance did the two trucks meet?
To answer this question, we will have to find the equations of the two lines and solve a system of equations with two variables.
We will find the equation of truck A with the help of the 2 given points. We will do the same for truck B. The two equations we obtain will form a system of equations with two variables. We will solve the system and obtain the meeting point between the two trucks.
In terms of time, we will obtain the value X and in terms of distance from Valencia, we will obtain the value Y.
If you are interested in this article, you might also be interested in the following articles:
