Identification of an Isosceles Triangle

When we have a triangle, we can identify that it is an isosceles if at least one of the following conditions is met:

1) If the triangle has two equal angles - The triangle is isosceles.
2) If in the triangle the height also bisects the angle of the vertex - The triangle is isosceles.
3) If in the triangle the height is also the median - The triangle is isosceles.
4) If in the triangle the median is also the bisector - The triangle is isosceles.

Detailed explanation

Start practice

Test yourself on types of triangles!

Fill in the blanks:

In an isosceles triangle, the angle between two ___ is called the "___ angle".

Practice more now

Identification of an Isosceles Triangle

Before we talk about how to identify an isosceles triangle, let's remember that it is a triangle with two sides (or edges) of the same length - This means that the base angles are also equal.
Moreover, in an isosceles triangle, the median of the base, the bisector, and the height are the same, that is, they coincide.

Let's see it illustrated

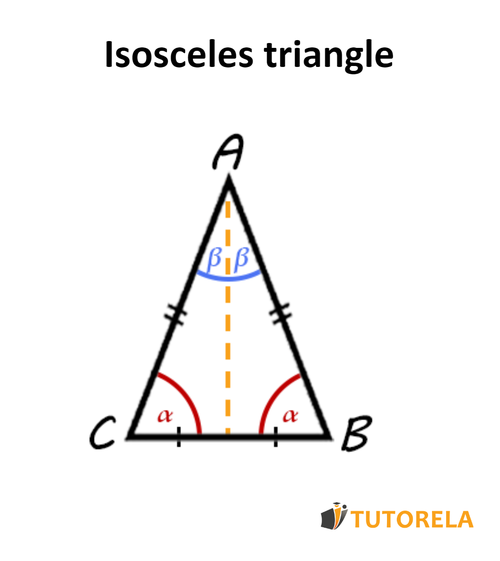
A - Identification of an isosceles triangle

These magnificent properties of the isosceles triangle cannot prove by themselves that it is an isosceles triangle.
So, how can we prove that our triangle is isosceles?

If at least one of the following conditions is met:
1) If our triangle has two equal angles - The triangle is isosceles.
This derives from the fact that the sides opposite to equal angles are also equal, therefore, if the angles are equal, the sides are too.

2) If in the triangle the height also bisects the vertex angle - The triangle is isosceles.
3) If in the triangle the height is also the median - The triangle is isosceles.
4) If in the triangle the median is also the angle bisector - The triangle is isosceles.
In fact, we can summarize guidelines $2$ and $4$ and write a single condition:
If two of these coincide - the median, the height, and the bisector - The triangle is isosceles.

Great, now you know how to identify isosceles triangles easily and quickly.

If you are interested in learning more about other angle topics, you can enter one of the following articles:

In the blog of Tutorela you will find a variety of articles about mathematics.

Examples and exercises with solutions for identifying an isosceles triangle

Exercise #1

Calculate the size of angle X given that the triangle is equilateral.

Video Solution

Step-by-Step Solution

Remember that the sum of angles in a triangle is equal to 180.

In an equilateral triangle, all sides and all angles are equal to each other.

Therefore, we will calculate as follows:

$x+x+x=180$

$3x=180$

We divide both sides by 3:

$x=60$

Answer

Exercise #2

What is the size of each angle in an equilateral triangle?

Video Solution

Step-by-Step Solution

To solve this problem, we'll follow these steps:

Step 1: Identify that an equilateral triangle has all sides of equal length, which implies its angles are also equal.
Step 2: Utilize the property that the sum of angles in any triangle is $180^\circ$ .
Step 3: Since each angle is equal in an equilateral triangle, divide the total sum of $180^\circ$ by 3.

Now, let's work through each step:
Step 1: In an equilateral triangle, all angles are equal in size.
Step 2: The sum of angles in any triangle is always $180^\circ$ .
Step 3: Divide $180^\circ$ by 3.

Calculating $180^\circ \div 3 = 60^\circ$ .

Therefore, the size of each angle in an equilateral triangle is $60^\circ$ .

Answer

Exercise #3

Which kind of triangle is given in the drawing?

Video Solution

Step-by-Step Solution

As we know that sides AB, BC, and CA are all equal to 6,

All are equal to each other and, therefore, the triangle is equilateral.

Answer

Equilateral triangle

Exercise #4

Given the size of the 3 sides of the triangle, is it an equilateral triangle?

Video Solution

Step-by-Step Solution

To determine if the triangle is equilateral, we need to check if all three sides of the triangle are equal.

The given side lengths are $2X$ , $12 - X$ , and $12 - X$ .

For the triangle to be equilateral, we must have the equality:

$2X = 12 - X$

Let's solve this equation:

$\begin{aligned} 2X &= 12 - X \\ 2X + X &= 12 \\ 3X &= 12 \\ X &= \frac{12}{3} \\ X &= 4 \end{aligned}$

Substitute $X = 4$ back into the expressions for the sides:

$2X = 2(4) = 8$
$12 - X = 12 - 4 = 8$
The third side, also $12 - X = 8$ .

The three calculated side lengths are $8$ , $8$ , and $8$ .

Since all three sides are equal, the triangle is an equilateral triangle.

Therefore, the answer is Yes, the triangle is equilateral.

Answer

Yes

Exercise #5

Is the triangle in the drawing an acute-angled triangle?

Video Solution

Step-by-Step Solution

To determine if the triangle is an acute-angled triangle, we need to understand the nature of its angles. In an acute-angled triangle, all three angles are less than $90^\circ$ . However, we do not have explicit angle measures or side lengths shown in the drawing. Instead, we assess the probable nature of the depicted triangle.

Given that an acute-angled triangle must have its largest angle smaller than $90^\circ$ , comparison property of triangle sides through Pythagorean type logic suggests that an acute triangle inequality $c^2 < a^2 + b^2$ (for sides $a$ , $b$ , and hypotenuse $c$ ) must hold.

In our problem, the depiction ultimately leads us to infer the implied relations among the triangle's angles. The given solution and analysis indicate it does not meet this criterion.

Hence, the triangle in the given drawing is not an acute-angled triangle, confirming the choice: No.