Scientific notation is the way of writing numbers that are very large or very small in an abbreviated form, using exponentiation.
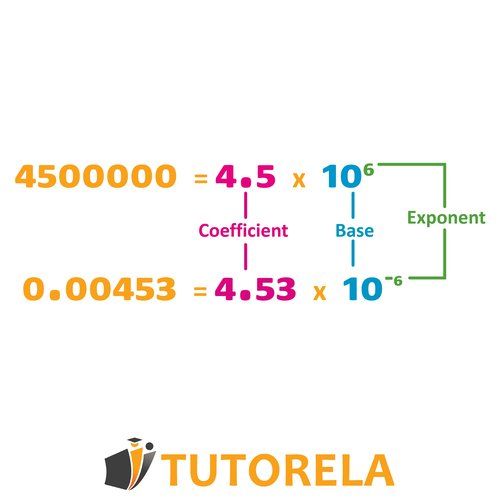
According to scientific notation, the number will be represented as the product of a certain number between and multiplied by raised to some power.
That is:
Small Numbers
Scientific Notation of Numbers
will be a number between and
If is a positive integer, the entire expression will be some number greater than
If is a negative integer, the entire expression will be some number less than
Small Numbers
Steps for the notation of very small numbers according to scientific notation:
- We will move the decimal point to the right until it is placed after a number that is less than .
- We will count how many steps we have moved the decimal point to the right, and the number of steps will be the exponent of , only this time, in negative.
- We will multiply the raised to the power we found (in negative) by our number and thus arrive at the scientific notation.
Scientific Notation of Numbers
What does it mean?
In certain scientific subjects such as, for example, biology and chemistry, there are extremely large or infinitesimally small numbers.
For example:
The mass of planet Earth is kg.
or
The radius of a carbon atom is m.
To express these numbers in a simple and practical way, without having to write a lot of digits, we can use powers.
Scientific notation is a system for expressing very large or very small numbers in a practical way.
According to scientific notation, the number will be represented as the product of a certain number between and multiplied by raised to some power.
That is:
will be a number between and
If is a positive integer, the whole expression will be some number greater than
If is a negative integer, the whole expression will be some number less than
Let's remember that, when we have a decimal number like, for example:
and we move the decimal point one step to the right, we are actually multiplying the number by .
That is, if we multiply
by
We will get:
Similarly, if we move the decimal point one step to the left, we are actually dividing the number by .
To write large and small numbers in a practical way we will use the powers of .
You'll catch on right away.
Let's take an example of a number that is not too large:
If we move our imaginary decimal point one step to the left, we are actually dividing the number by .
Therefore, to not alter the numerical value we must immediately multiply it by .
That is:
If we move the point another step back, we must multiply by .
That is:
We know that, can be written as
Therefore, we can express as:
Similarly, if we take a larger number, for example:
We can say it is equivalent to:
We know that, is equivalent to
Therefore:
So how can we write numbers using scientific notation without getting confused?
Small Numbers
Steps for the notation of very large numbers according to scientific notation:
- We will move the decimal point to the right until it is placed after a number that is less than .
- We will count how many steps we have moved the decimal point to the right. The number of steps taken will be the exponent of , only this time, in negative.
- We will multiply the raised to the power we found (in negative) by our number and that will give us the scientific notation.
Let's take the following number as an example:

We moved the decimal point to the right until it was behind a number greater than .
We counted the number of steps taken and got . Since we moved the decimal point to the right, the exponent will be the number of steps taken in negative, that is .
Therefore, we will obtain:








