Addition Subtraction Equations Practice Problems

Master solving equations using addition and subtraction methods with step-by-step practice problems. Learn to isolate variables by adding or subtracting same values from both sides.

📚Master Equation Solving with Addition and Subtraction

Apply addition and subtraction properties to solve linear equations
Isolate variables by adding or subtracting same values from both sides
Solve equations like X+5+2=3 and X+7-4=10 step by step
Understand why adding same numbers to both sides preserves equality
Practice identifying which operation to use for equation solving
Build confidence solving one-variable linear equations systematically

Understanding Solving Equations by using Addition/ Subtraction

Complete explanation with examples

This method allows us to add or subtract the same element from both sides of the equation without changing the final result, that is, the outcome of the equation will not be affected by the fact that we have added or subtracted the same element from both sides.

Solving Equations by Adding or Subtracting the Same Number from Both Sides

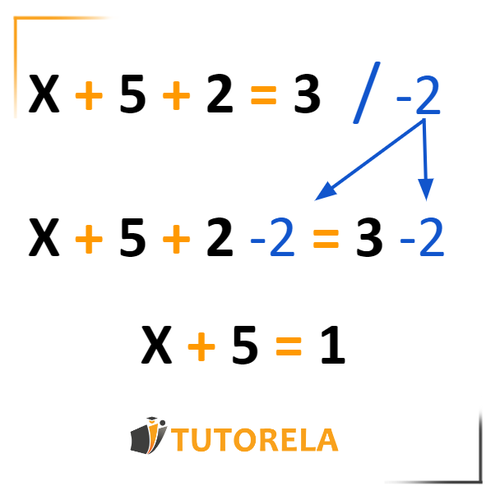
Let's see what the logic of this method is:

José and Isabel, for example, are twin siblings who receive their weekly allowance for the first time.

José and Isabel receive $10$ euros each, so at this moment they have exactly $10$ euros per person.

After a month, each has received another $2$ euros, so now each has $12$ euros.

We see that adding $2$ euros to the amount each of them had has not affected the equivalence between them: both still have the same amount of money.

Detailed explanation

Practice Solving Equations by using Addition/ Subtraction

Test your knowledge with 27 quizzes

Solve for X:

$$ x - 7 = 14 $$

Examples with solutions for Solving Equations by using Addition/ Subtraction

Step-by-step solutions included

Exercise #1

Solve for X:

$x + 9 = 15$

Step-by-Step Solution

Step-by-step solution:

1. Begin with the equation: $x + 9 = 15$

2. Subtract 9 from both sides: $x + 9 - 9 = 15 - 9$ , which simplifies to $x = 6$

Answer:

Video Solution

Exercise #2

$11=a-16$

$a=\text{?}$

Step-by-Step Solution

To find the value of $a$ , we must solve the given linear equation:

$11 = a - 16$

We aim to isolate $a$ by performing operations that maintain the balance of the equation. Currently, $a$ is being decreased by 16. To reverse this, we need to add 16 to both sides.

Step-by-step:

Start with the given equation: $11 = a - 16$ .
Add 16 to both sides to start isolating $a$ :

$11 + 16 = a - 16 + 16$

This simplifies to:

$27 = a$

Thus, the value of $a$ is 27.

Therefore, the solution to the equation $11 = a - 16$ is $a = 27$ .

Answer:

$27$

Video Solution

Exercise #3

Solve for A:

$a-5=10$

Step-by-Step Solution

To solve for $a$ , we need to isolate it on one side of the equation. Starting with:

$a-5=10$

Add $5$ to both sides to get:

$a-5+5=10+5$

This simplifies to:

$a=15$

Therefore, the solution is $a = 15$ .

Answer:

$15$

Exercise #4

Solve for B:

$b+6=14$

Step-by-Step Solution

To solve for $b$ , we need to isolate it on one side of the equation. Starting with:

$b+6=14$

Subtract $6$ from both sides to get:

$b+6-6=14-6$

This simplifies to:

$b=8$

Therefore, the solution is $b = 8$ .

Answer:

$8$

Exercise #5

Solve for X:

$x + 3 = 7$

Step-by-Step Solution

To solve for $x$ , start by isolating $x$ on one side of the equation:
Subtract $3$ from both sides:
$x + 3 - 3 = 7 - 3$ simplifies to
$x = 4$ .

Answer:

Video Solution

Frequently Asked Questions

Everything you need to know about Solving Equations by using Addition/ Subtraction

How do you solve equations using addition and subtraction?

To solve equations using addition and subtraction, add or subtract the same number from both sides of the equation. This preserves equality while helping isolate the variable. For example, in X+5+2=3, subtract 2 from both sides to get X+5=1.

Why can you add the same number to both sides of an equation?

Adding the same number to both sides maintains the balance of the equation, just like adding the same amount of money to two equal bank accounts keeps them equal. This fundamental property allows us to manipulate equations without changing their solutions.

What's the difference between adding and subtracting in equation solving?

The choice depends on what you need to isolate: • If you have +5 on one side, subtract 5 from both sides • If you have -3 on one side, add 3 to both sides • Always do the opposite operation to cancel out unwanted terms

How do you know which operation to use when solving equations?

Look at the term you want to eliminate and use the opposite operation. If the equation has +7, subtract 7 from both sides. If it has -4, add 4 to both sides. This cancels out the unwanted term and isolates your variable.

What are common mistakes when solving equations with addition and subtraction?

Common mistakes include: forgetting to apply the operation to both sides, using the wrong operation (adding instead of subtracting), and making arithmetic errors. Always check your answer by substituting back into the original equation.

Can you solve X+7-4=10 step by step?

Step-by-step solution for X+7-4=10: 1. Simplify the left side: X+3=10 2. Subtract 3 from both sides: X+3-3=10-3 3. Simplify: X=7 4. Check: 7+7-4=10 ✓

When should students learn addition subtraction equation solving?

Students typically learn addition and subtraction equation solving in middle school algebra, usually grades 6-8. This foundational skill prepares them for more complex equation types and is essential before learning multiplication and division methods.

What real world problems use addition subtraction equations?

Real-world applications include budgeting (income + savings - expenses = remaining money), distance problems (starting point + distance traveled = final position), and temperature changes (initial temp + increase - decrease = final temp). These equations model everyday mathematical relationships.

More Solving Equations by using Addition/ Subtraction Questions

Click on any question to see the complete solution with step-by-step explanations

Solving Equations by using Addition/ Subtraction

Continue Your Math Journey

Master Solving Equations by using Addition/ Subtraction first, then advance to these related topics that build on your fraction skills

Topics Learned in Later Sections

Solving Equations by Multiplying or Dividing Both Sides by the Same Number Solving Equations by Simplifying Like Terms Solving Equations Using the Distributive Property Solution by all methods First-degree equations with one unknown Solution of an equation

Practice by Question Type

Choose your preferred learning style and practice format for fraction problems

Complete the missing number Equations with variables on both sides Exercises on Both Sides (of the Equation) More than Two Terms One sided equations Monomial Solving an equation by multiplying/dividing both sides Solving an equation using all techniques Solving an equation with fractions Simplifying expressions Test if the coefficient is different from 1 Binomial Using variables Worded problems