First-degree equations with one unknown

What is an equation with one unknown?

Equations are algebraic expressions containing numbers and unknowns. It is important to differentiate these two groups: the numbers are fixed values while the unknowns, as their name indicates, represent unknown values (at least at the beginning), and in most cases we are asked to find out what this value is.
For example:

A1 - First-degree equations with one unknown

What do we do with the equations?

When we are given an exercise that contains an equation with an unknown, our goal is to solve the equation, that is, to find a solution to the equation. What does it mean to find the solution to an equation? The idea is to find the value of the unknown with the goal of making both sides of the equation equal.

When we have equations that have the same solution, they will be called equivalent equations.

When first degree equations include fractions, and the unknown is in the denominator, it is important to keep in mind the domain of the function

Detailed explanation

Start practice

Test yourself on linear equations!

Solve the equation

$$ 5x-15=30 $$

Practice more now

Principles and methods for solving first-degree equations with one unknown

Examples and exercises

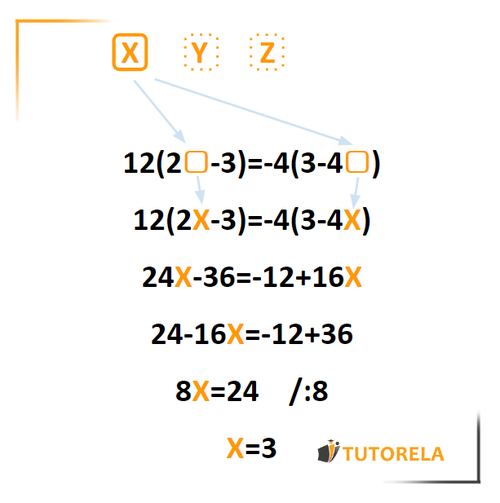
Exercise 1

Solve the following equation:

$12\left(2X-3\right)=-4\left(3-4X\right)$

Solution:

To solve the equation, we first make the products of the two sides of the equation:

$24X-36=-12+16X$

Next we will group the like terms, so that on the left side of the equation all the unknowns appear, while on the right side of the equation the numbers appear. Remember, when transposing the terms from one side of the equation to the other, their sign will change. That is, if it is adding, it will go to the other side subtracting, and vice versa.

$24X-16X=-12+36$

Then we reduce the like terms:

$8X=24$

Now, to find the value of the unknown, we divide both sides of the equation by 8 and get:

$8X/8=24/8$

$X=3$

Thus, $X=3$ is the solution of the equation.

Answer:

$X=3$

Exercise 2

Solve the following equation:

$8\left(2-5X\right)-12\left(1-X\right)=0$

To solve this equation, we first do the product of the left side of the equation, obtaining:

$16-40X-12+12X=0$

Next we group the like terms, so that on the left side of the equation all the unknowns appear, while on the right side of the equation the numbers will appear. Remember, when transposing the terms from one side of the equation to the other, the sign of the terms will change.

$-40X+12X=12-16$

The next step is to reduce the like terms:

$-28X=-4$

Now, to find the value of the unknown, we divide the two sides of the equation by (-28) and we will get:

$-28X/-28=-4/-28$

And finally we reduce the fraction:

$X=\frac{4}{28}=\frac{1}{7}$

Answer:

$X=\frac{1}{7}$

Join Over 30,000 Students Excelling in Math!

Endless Practice, Expert Guidance - Elevate Your Math Skills Today

Test your knowledge

Question 1

$$ 4x:30=2 $$

Question 2

Solve the equation

$$ 7x+5.5=19.5 $$

Question 3

Solve the equation

$$ 20:4x=5 $$

Exercise 3

Solve the following equation:

$-6\left(-X-1\right)+10\left(2-X\right)=16$

To solve the equation, we first make the products of the two sides of the equation:

$6X+6+20-10X=16$

We then group the like terms together, so that on the left side of the equation all the unknowns appear, while on the right side of the equation the numbers appear. Remember, when transposing the terms from one side of the equation to the other, their sign will change. That is, if it is adding, it will go to the other side subtracting, and vice versa.

$6X-10X=16-6-20$

The next step is to reduce the like terms:

$-4X=-10$

Now, to find the value of the unknown, we divide both sides of the equation by (-4), and we will get:

$-4X/-4=-\frac{10}{-4}$

$X=\frac{10}{4}=2.5$

Answer:

$X=2.5$

Exercise 4

Solve the following equation:

$3\frac{1}{2}\cdot y=21$

Solution

Note that:

$3\frac{1}{2}=\frac{7}{2}$

Thus the equation is equivalent to:

$\frac{7}{2}\cdot y=21$

Now, we divide by 7/2 both sides of the equation and get:

$y=\frac{21}{\frac{7}{2}}=6$

$y=6$

Answer

$y=6$

Do you know what the answer is?

Question 1

Solve the equation

$8x\cdot10=80$

Question 2

$$ 5x=0 $$

Question 3

$$ 5x=1 $$

What is the value of x?

Exercise 5

Solve the following equation:

$4\frac{1}{3}\cdot x=21\frac{2}{3}$

Solution

Note that:

$4\frac{1}{3}=\frac{13}{3}$

$21\frac{2}{3}=\frac{65}{3}$

Thus, the equation is equivalent to:

$\frac{13}{3}\cdot x=\frac{65}{3}$

Divide both sides of the equation by:

$\frac{13}{3}$

to simplify

$x=\frac{\frac{65}{3}}{\frac{13}{3}}$

$x=5$

Answer

$x=5$

Exercise 6

Solve the following equation:

$3x+4+x+1=9$

Solution

Next we group the like terms, so that on the left side of the equation all the unknowns appear, while on the right side of the equation the numbers appear.

$3x+x=9-4-1$

We add the like terms:

$4x=4$

We divide both sides of the equation by $4$

$4x/4=4/4$

Answer

$x=1$

Check your understanding

Question 1

Find the value of the parameter X:

$$ x+5=8 $$

Question 2

Solve for X:

$$ 3+x=4 $$

Question 3

Solve for X:

$$ 5-x=4 $$

Exercise 8

Solve the following problem:

What is the domain of application of the equation?

$\frac{xyz}{2(3+y)+4}=8$

Solution

We must calculate when the denominator on the right hand side of the equation equals zero, i.e:

$2\left(3+y\right)+4=0$

We multiply by $2$ in the two elements of the parentheses.

$6+2y+4=0$

We add accordingly

$10+2y=0$

We go to $10$ to the right hand section

$2y=-10$

Divide by $2$

$y=-5$

$y\ne-5$

If $Y$ is equal to minus $5$ then the denominator is equal to $0$ and the exercise has no solution.

Answer

$y\ne-5$

Questions on the subject

What is a first degree equation with one unknown?

It is a mathematical expression consisting of an unknown or variable and numbers in which the value of the variable must be found, which is generally denoted by $X$ .

Examples

a) $3x-5=2x+4$ .

b) $4-x=10$ .

c) $4(x-4)+2=2x$ .

Do you think you will be able to solve it?

Question 1

Solve for X:

$$ -8-x=-5 $$

Question 2

Find the value of the parameter X

$$ -8-x=5 $$

Question 3

Solve for X:

$$ -5+x=-3 $$

How to solve first degree equations with one unknown?

Isolating the unknown, that is, leaving it alone somewhere in the equality.

What are first degree equations with two unknowns?

It is a mathematical expression consisting of two unknowns or variables and numbers in which the value of the variables must be found, which are generally denoted by $X$ and $Y$ .

Test your knowledge

Question 1

Solve for X:

$$ 5x=25 $$

Question 2

Solve for X:

$$ 6x=72 $$

Question 3

Solve the equation

$$ 5x-15=30 $$

How to clear an unknown?

Isolating the variable or unknown using operations such as addition, subtraction, multiplication and division.

Do you know what the answer is?

Question 1

$$ 4x:30=2 $$

Question 2

Solve the equation

$$ 7x+5.5=19.5 $$

Question 3

Solve the equation

$$ 20:4x=5 $$

Examples with solutions for Linear Equations

Exercise #1

Solve the equation

$5x-15=30$

Video Solution

Step-by-Step Solution

We start by moving the sections:

5X-15 = 30
5X = 30+15

5X = 45

Now we divide by 5

X = 9

Answer

$x=9$

Exercise #2

Solve the equation

$20:4x=5$

Video Solution

Step-by-Step Solution

To solve the exercise, we first rewrite the entire division as a fraction:

$\frac{20}{4x}=5$

Actually, we didn't have to do this step, but it's more convenient for the rest of the process.

To get rid of the fraction, we multiply both sides of the equation by the denominator, 4X.

20=5*4X

20=20X

Now we can reduce both sides of the equation by 20 and we will arrive at the result of:

X=1

Answer

$x=1$

Exercise #3

Find the value of the parameter X

$\frac{1}{3}x+\frac{5}{6}=-\frac{1}{6}$

Video Solution

Step-by-Step Solution

First, we will arrange the equation so that we have variables on one side and numbers on the other side.

Therefore, we will move $\frac{5}{6}$ to the other side, and we will get

$\frac{1}{3}x=-\frac{1}{6}-\frac{5}{6}$

Note that the two fractions on the right side share the same denominator, so you can subtract them:

$\frac{1}{3}x=-\frac{6}{6}$

Observe the minus sign on the right side!

$\frac{1}{3}x=-1$

Now, we will try to get rid of the denominator, we will do this by multiplying the entire exercise by the denominator (that is, all terms on both sides of the equation):

$1x=-3$

$x=-3$

Answer

-3

Exercise #4

Solve the equation

$4\frac{1}{3}\cdot x=21\frac{2}{3}$

Video Solution

Step-by-Step Solution

We have an equation with a variable.

Usually, in these equations, we will be asked to find the value of the missing (X),

This is how we solve it:

To solve the exercise, first we have to change the mixed fractions to an improper fraction,

So that it will then be easier for us to solve them.

Let's start with the four and the third:

To convert a mixed fraction, we start by multiplying the whole number by the denominator

4*3=12

Now we add this to the existing numerator.

12+1=13

And we find that the first fraction is 13/3

Let's continue with the second fraction and do the same in it:
21*3=63

63+2=65

The second fraction is 65/3

We replace the new fractions we found in the equation:

13/3x = 65/3

At this point, we will notice that all the fractions in the exercise share the same denominator, 3.

Therefore, we can multiply the entire equation by 3.

13x=65

Now we want to isolate the unknown, the x.

Therefore, we divide both sides of the equation by the unknown coefficient -
13.

63:13=5

x=5

Answer

$x=5$

Exercise #5

The area of the rectangle below is equal to 22x.

Calculate x.

Video Solution

Step-by-Step Solution

The area of the rectangle is equal to the length multiplied by the width.

Let's list the known data:

$22x=\frac{1}{2}x\times(x+8)$

$22x=\frac{1}{2}x^2+\frac{1}{2}x8$

$22x=\frac{1}{2}x^2+4x$

$0=\frac{1}{2}x^2+4x-22x$

$0=\frac{1}{2}x^2-18x$

$0=\frac{1}{2}x(x-36)$

For the equation to be equal, x needs to be equal to 36

Answer

$x=36$

Start practice