In this article, we will learn what area is, and understand how it is calculated for each shape, in the most practical and simple way there is.
Shall we start?
Area
What is the area?
Area is the definition of the size of something. In mathematics, which is precisely what interests us now, it refers to the size of some figure.
In everyday life, you have surely heard about area in relation to the surface of an apartment, plot of land, etc.
In fact, when they ask what the surface area of your apartment is, they are asking about its size and, instead of answering with words like "big" or "small" we can calculate its area and express it with units of measure. In this way, we can compare different sizes.
Units of measurement of area
Large areas such as apartments are usually measured in meters, therefore, the unit of measurement will be square meter.
On the other hand, smaller figures are generally measured in centimeters, that is, the unit of measurement for the area will be square centimeter.
Remember:
Units of measurement for the area in
Units of measurement for the area
Test yourself on area of the square!
Look at the rectangle ABCD below.
Side AB is 6 cm long and side BC is 4 cm long.
What is the area of the rectangle?
Area
Now we will learn to calculate the area of (almost) all the shapes we know! Are we ready?
Area of the Square
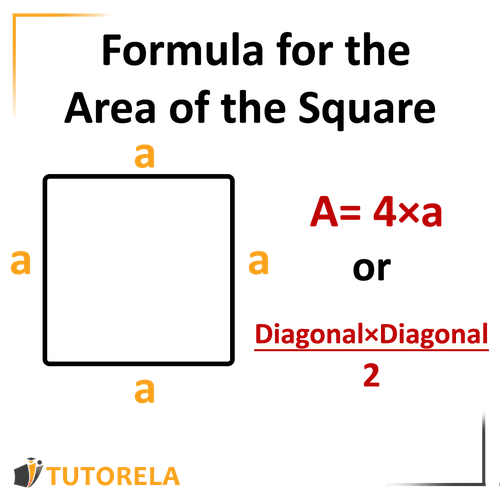
Side of the square
We will multiply the side of the square by itself
Another way:
For more information, enter the link of Area of a square
Look at the rectangle ABCD below.
Side AB is 4.5 cm long and side BC is 2 cm long.
What is the area of the rectangle?
Look at rectangle ABCD below.
Side AB is 10 cm long and side BC is 2.5 cm long.
What is the area of the rectangle?
The triangle ABC is given below.
AC = 10 cm
AD = 3 cm
BC = 11.6 cm
What is the area of the triangle?
Area of the Rectangle
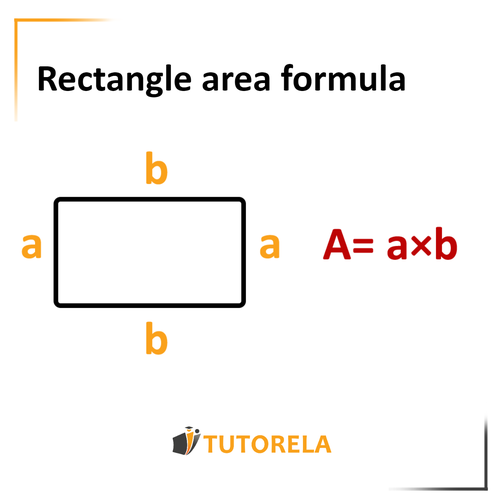
We will multiply one side of the rectangle by the adjacent side (the side with which it forms a degree angle)
For more information, enter the link of Rectangle area
Area of the triangle
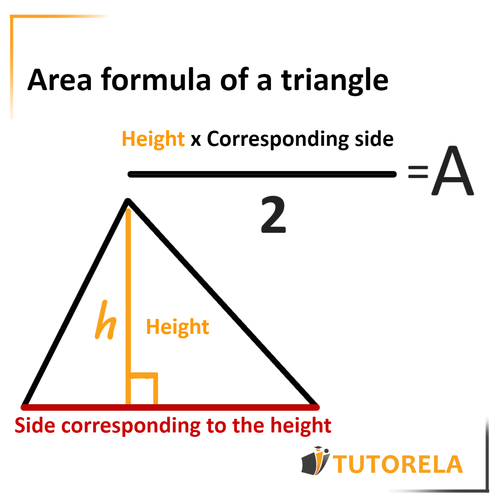
We will multiply the height by the corresponding side - that is, the side with which it forms a degree angle and divide the product by .
For more information, enter the link to Triangle Area
What is the area of the given triangle?
What is the area of the triangle in the drawing?
Given the trapezoid:
What is the area?
Area of the Rhombus
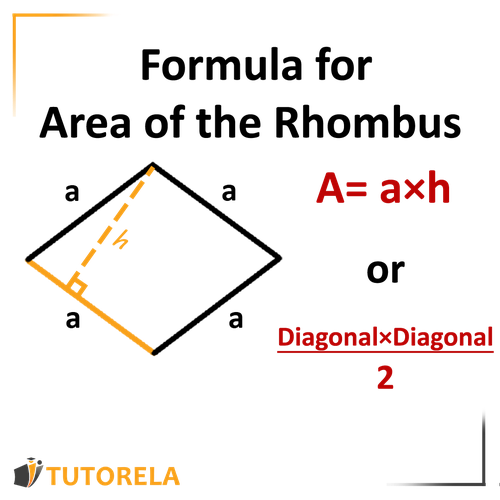
–> Side of the rhombus
–> Height
We will multiply the height by the corresponding side, that is, the side with which it forms a right angle of degrees.
Another way :
For more information, enter the link of Rhombus area
Area of the parallelogram
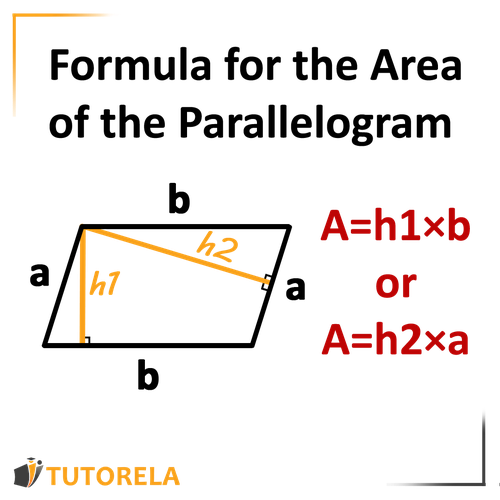
–> Height
–> The side that forms a degree angle with the height .
We will multiply the height by the side to which the height reaches and forms with it a degree angle.
For more information, enter the link of Parallelogram area
Look at the circle in the figure:
\( \)
The radius of the circle is 4.
What is its area?
Look at the circle in the figure:
The radius is equal to 7.
What is the area of the circle?
Given the rhombus in the drawing:
What is the area?
Area of the Circle
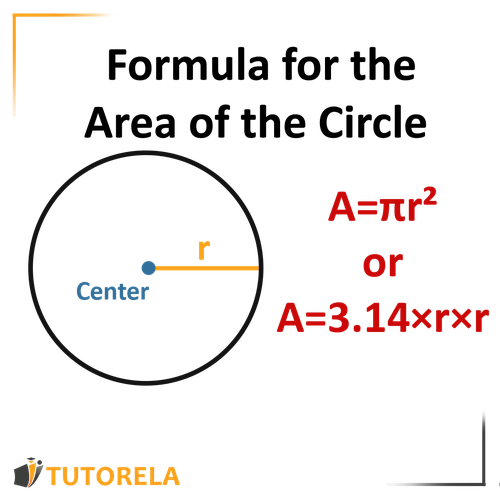
The radius of the circumference
PI
It will be calculated as the number
We will multiply PI by the radius of the circumference squared, that is
Or, more simply, the formula is:
For more information, enter the link of Circle area
Area of the trapezoid
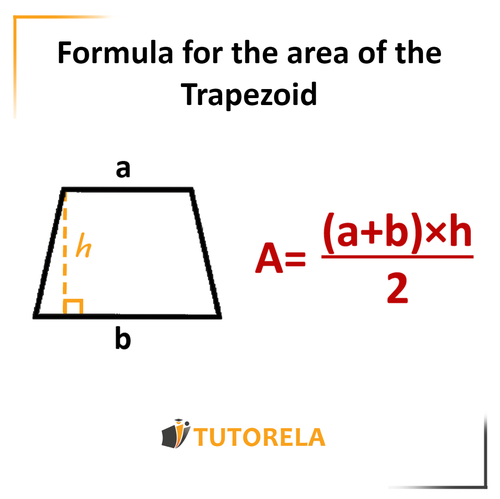
We will add the bases and multiply the result by the height of the trapezoid.
We will divide the result by .
For more information, enter the link of Trapezoid area
Given the rhombus in the drawing:
What is the area?
The rhombus in the diagram has an area of 24 cm².
What is the value of X?
Look at the deltoid in the figure:
What is its area?
Area of the Kite
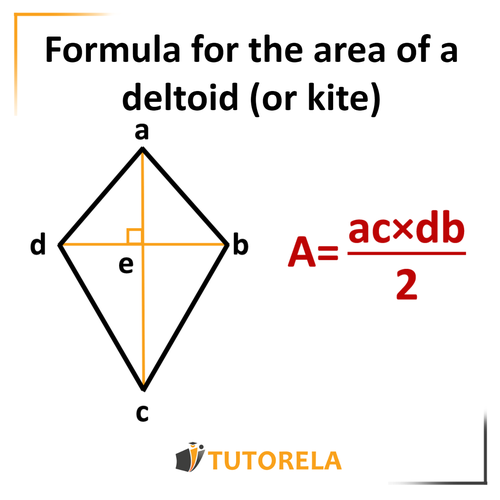
We will multiply the diagonals and divide by .
For more information, enter the link of Area of the kite
Area of Composite Figures
You don't have to worry about this pair of terms - composite figures. They are not called composite because they are complicated or difficult, but rather, they are composite figures because they are really made up of several figures that you already know.
The great key to calculating the area of this type of figures is to separate them into several simple figures on which you know how to calculate their area.
Let's look at an example
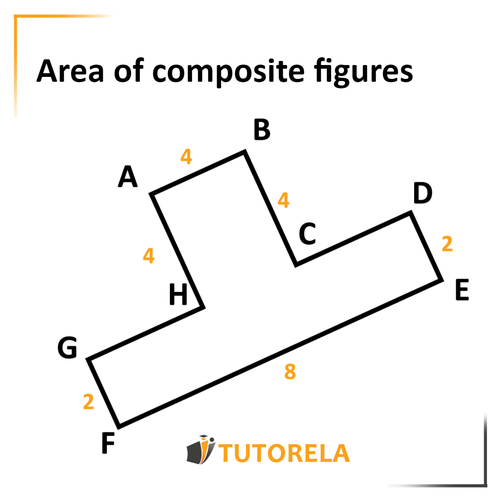
At first glance, it might scare us a bit since the figure seems very strange. But, very quickly we will remember the suggestion that we have written here above and apply it.
We will realize that we can divide the composite figure into two that we know and know how to calculate their area, rectangle and square.
We will calculate the area of each figure separately and then add them together.
In this way, we will obtain the area of the entire figure.
Look at the deltoid in the figure:
What is its area?
Given the rhombus in the drawing:
What is the area?
Look at the rectangle ABCD below.
Side AB is 6 cm long and side BC is 4 cm long.
What is the area of the rectangle?
What is the difference between surface area and volume?
To understand the difference, let's remember a daily term we use in another context: superficial.
Superficial implies something or someone without depth, so, in geometry, the surface indicates the size of something flat, without depth. For example, if we draw a ball and paint it, that painted part would be its surface.
On the other hand, volume refers to the actual size of the ball, the space that we could fill inside it.
Volume is not the surface on the sheet of paper, but, really the size we can see (in a three-dimensional way) - the space it occupies in space.
The calculation of volume differs from the calculation of the surface.

Examples and exercises with solutions for area calculation
Exercise #1
Look at the rectangle ABCD below.
Side AB is 6 cm long and side BC is 4 cm long.
What is the area of the rectangle?
Video Solution
Step-by-Step Solution
Remember that the formula for the area of a rectangle is width times height
We are given that the width of the rectangle is 6
and that the length of the rectangle is 4
Therefore we calculate:
6*4=24
Answer
24 cm²
Exercise #2
Look at the rectangle ABCD below.
Side AB is 4.5 cm long and side BC is 2 cm long.
What is the area of the rectangle?
Video Solution
Step-by-Step Solution
We begin by multiplying side AB by side BC
We then substitute the given data and we obtain the following:
Hence the area of rectangle ABCD equals 9
Answer
9 cm²
Exercise #3
Look at rectangle ABCD below.
Side AB is 10 cm long and side BC is 2.5 cm long.
What is the area of the rectangle?
Video Solution
Step-by-Step Solution
Let's begin by multiplying side AB by side BC
If we insert the known data into the above equation we should obtain the following:
Thus the area of rectangle ABCD equals 25.
Answer
25 cm²
Exercise #4
The triangle ABC is given below.
AC = 10 cm
AD = 3 cm
BC = 11.6 cm
What is the area of the triangle?
Video Solution
Step-by-Step Solution
The triangle we are looking at is the large triangle - ABC
The triangle is formed by three sides AB, BC, and CA.
Now let's remember what we need for the calculation of a triangular area:
(side x the height that descends from the side)/2
Therefore, the first thing we must find is a suitable height and side.
We are given the side AC, but there is no descending height, so it is not useful to us.
The side AB is not given,
And so we are left with the side BC, which is given.
From the side BC descends the height AD (the two form a 90-degree angle).
It can be argued that BC is also a height, but if we delve deeper it seems that CD can be a height in the triangle ADC,
and BD is a height in the triangle ADB (both are the sides of a right triangle, therefore they are the height and the side).
As we do not know if the triangle is isosceles or not, it is also not possible to know if CD=DB, or what their ratio is, and this theory fails.
Let's remember again the formula for triangular area and replace the data we have in the formula:
(side* the height that descends from the side)/2
Now we replace the existing data in this formula:
Answer
17.4
Exercise #5
What is the area of the given triangle?
Video Solution
Step-by-Step Solution
This question is a bit confusing. We need start by identifying which parts of the data are relevant to us.
Remember the formula for the area of a triangle:
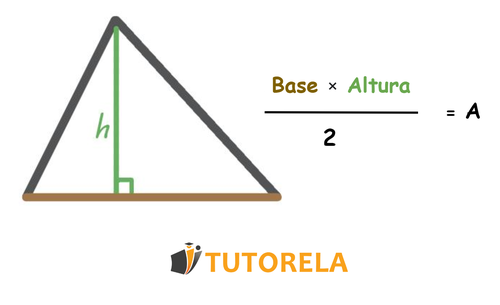 The height is a straight line that comes out of an angle and forms a right angle with the opposite side.
The height is a straight line that comes out of an angle and forms a right angle with the opposite side.
In the drawing we have a height of 6.
It goes down to the opposite side whose length is 5.
And therefore, these are the data points that we will use.
We replace in the formula:
Answer
15
Look at the rectangle ABCD below.
Side AB is 4.5 cm long and side BC is 2 cm long.
What is the area of the rectangle?
Look at rectangle ABCD below.
Side AB is 10 cm long and side BC is 2.5 cm long.
What is the area of the rectangle?
The triangle ABC is given below.
AC = 10 cm
AD = 3 cm
BC = 11.6 cm
What is the area of the triangle?
More Questions
Area of a Parallelogram
Area of a Rectangle
- Rectangle Area: Solving with Width x and Length x/2 When x=4
- Calculate Rectangle Area: 3² cm Width × 1.5 cm Length
- Calculate Rectangle Area: 15 cm × 3 cm Dimensions
- Calculate Rectangle Area with Dimensions 2x and (2x-8): Variable Expression Problem
- Calculate Rectangle Area: Finding x(x-4) with Variable Dimensions
Area of a Trapezoid
- Solve for X: Trapezoid with Area 60 and Bases 8 and 14
- Calculate Trapezoid Height X: Area 30 with Bases 3.5 and 7.5
- Calculate X in Trapezoid: Given Height 5 and Base 7
- Calculate Trapezoid Area: Finding Space Between 9.6 and 13 Units
- Calculate Trapezoid Area: Finding Space with 5-Unit Top Base and 6-Unit Height
Area of a Triangle
Area of the Square
- Square Geometry: Comparing Diagonal Sums vs. Triple Side Length
- Square Geometry Problem: Comparing Diagonal Sums vs Side Lengths in a 4-Unit Square
- Compare Square Diagonals vs Sides: 11-Unit Square Analysis
- Square Geometry Problem: Comparing Diagonal and Side Length Sums
- Square Geometry: Comparing Diagonal Sum vs Side Lengths in a 6-Unit Square
Area of a Deltoid
- Calculate Triangle Ratios in a Deltoid: Using the 1:5 Point Relationship
- Deltoid Geometry: Calculate the 1:3 Point Division and Triangle Area Ratio
- Deltoid Area Calculation: Using 4cm and 5cm Diagonals
- Deltoid Diagonal Calculation: Finding AC When Area = 24cm² and DB = 4
- Calculate the Second Diagonal in a Deltoid with Area 18 cm² and First Diagonal 3 cm
Area of a Circle
- Circle-Parallelogram Tangency Problem: Finding Area of Blue Regions with 25.13 Circumference
- Calculate Circle Area: Finding the Area When Diameter = 13
- Calculate the Area of a Semicircle with Radius 14 Units
- Find X in a Right-Angled Trapezoid: Area 2.5x² with Circle Diameter Relationship
- Area Calculation: 4×8 Rectangle with Four Semicircles
- Area
- Trapezoids
- Symmetry in Trapezoids
- Diagonals of an isosceles trapezoid
- Area of a trapezoid
- Perimeter of a trapezoid
- Types of Trapezoids
- Isosceles Trapezoid
- Parallelogram
- The area of a parallelogram: what is it and how is it calculated?
- Perimeter of a Parallelogram
- Identifying a Parallelogram
- Rotational Symmetry in Parallelograms
- From the Quadrilateral to the Parallelogram
- Kite
- Area of a Deltoid (Kite)
- Congruent Triangles
- Parallel lines
- Angles In Parallel Lines
- Alternate angles
- Corresponding angles
- Collateral angles
- Vertically Opposite Angles
- Adjacent angles
- The Pythagorean Theorem
- Elements of the circumference
- Circle
- Diameter
- Pi
- Area of a circle
- Distance from a chord to the center of a circle
- Chords of a Circle
- Central Angle in a Circle
- Arcs in a Circle
- Perpendicular to a chord from the center of a circle
- Inscribed angle in a circle
- Tangent to a circle
- The Circumference of a Circle
- The Center of a Circle
- Radius
- How is the radius calculated using its circumference?
- Rectangle
- From a Quadrilateral to a Rectangle
- From a Parallelogram to a Rectangle
- Calculating the Area of a Rectangle
- The perimeter of the rectangle
- Congruent Rectangles
- The sides or edges of a triangle
- Similarity of Triangles and Polygons
- Triangle similarity criteria
- Triangle Height
- Midsegment
- Midsegment of a triangle
- Midsegment of a trapezoid
- The Sum of the Interior Angles of a Triangle
- Exterior angles of a triangle
- Relationships Between Angles and Sides of the Triangle
- Relations Between The Sides of a Triangle
- Square
- Area of a square
- From Parallelogram to Square
- Rhombus, kite, or diamond?
- Diagonals of a Rhombus
- Lines of Symmetry in a Rhombus
- From Parallelogram to Rhombus
- The Area of a Rhombus
- Perimeter
- Triangle
- Types of Triangles
- Obtuse Triangle
- Equilateral triangle
- Identification of an Isosceles Triangle
- Scalene triangle
- Acute triangle
- Isosceles triangle
- The Area of a Triangle
- Area of a right triangle
- Area of Isosceles Triangles
- Area of a Scalene Triangle
- Area of Equilateral Triangles
- Perimeter of a triangle
- Cylinder Surface Area
- Cylinder Volume
- Cuboids
- Cubes
- How to calculate the surface area of a rectangular prism (orthohedron)
- How to calculate the volume of a rectangular prism (orthohedron)
- Lateral surface area of a rectangular prism
- Right Triangular Prism
- Bases of the Right Triangular Prism
- The lateral faces of the prism
- Lateral Edges of a Prism
- Height of a Prism
- The volume of the prism
- Surface area of triangular prisms
- Areas of Polygons for 7th Grade
- Right Triangle
- Area of a right-angled trapezoid
- Area of an isosceles trapezoid
- Corresponding exterior angles
- Alternate interior angles
- Median in a triangle
- Center of a Triangle - The Centroid - The Intersection Point of Medians
- How do we calculate the area of complex shapes?
- How to calculate the area of a triangle using trigonometry?
- How do we calculate the perimeter of polygons?
- All terms in triangle calculation
- Parts of a Circle
- Circuit Components
- Diagonals in a rectangle
- Symmetry in a kite









