Pi

If this article interests you, you may also be interested in the following articles:

• The circumference
• The center of the circumference
• Circle
• Radius
• Diameter
• The perimeter of the circle
• Circular area
• Arcs in a circle
• Chords in a circle
• Central angle in a circle
• Perpendicular to the chord from the center of the circle
• Inscribed angle in a circle

On Tutorela website you will find a variety of articles on mathematics.

What does the number Pi represent?

Pi is a number that represents the constant relationship between the circumference and its diameter.

What is the value of the number Pi?

The value of Pi is approximately $3.14$ and its decimal representation includes an infinite number of digits.

What are the characteristics of the number Pi?

Pi is a pure number, and it is also irrational.

Expression of the number "Pi" as a fraction?

The fraction of Pi is $\frac{22}{7}$ (approximately).

Problem

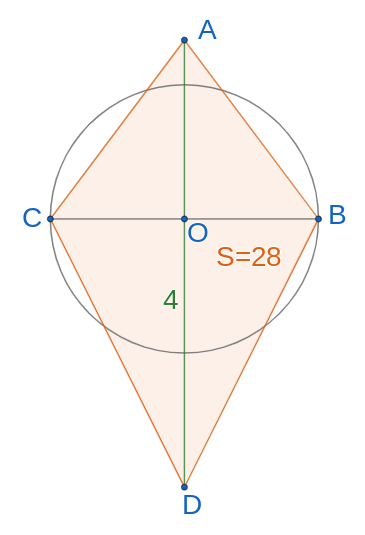
Given the deltoid $ABCD$ and the circle whose center $O$ is on the diagonal $BC$

The area of the deltoid is $28\operatorname{cm}²$

$AD=4$

What is the area of the circle?

Solution

Area of the deltoid $ABCD$

$28=\frac{AD\cdot CB}{2}=2CB$

Divided by $2$

$14=CB$

The diameter of the circle is $CB$

Diameter times half is equal to radius

Replace accordingly

$\frac{1}{2}\cdot14=7$

$A=\pi r^2=\pi\cdot7^2$

$A=49\pi$

Answer

$49\pi$

Question

Given the parts of the circle shown in the figure (white)

Diameter of the circle $11\operatorname{cm}$

How much is the area of the shaded parts together?

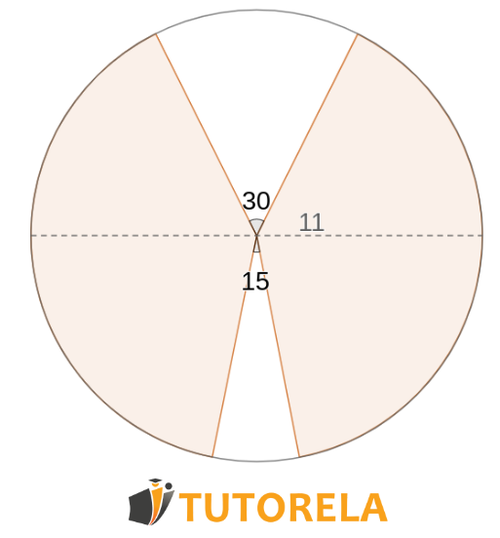
The area of the parts is like the area of the circle minus the two sections, one of which extends by an angle of $30°$ and the other by an angle of $15°$

In the same way we can look at the parts like this:

Then its area is the area of the circle minus the area of the section extended by an angle of $(45°)$

Or it is just a cut area extending by $(360°)$ degrees minus $(45°)$ degrees, i.e.,$(315°)$ degrees.

$A=\frac{315°}{360°}\cdot\pi\cdot(\frac{11}{2})^2=83.11$

Answer

$83.11\operatorname{cm}²$

Question

What is the area of a slice of pizza whose diameter is $45\operatorname{cm}$ after dividing into $8$ slices?

Solution

Pizza divided by: $8$ slices

In other words, the area of a slice of pizza is $\frac{1}{8}$

$Apizza=\pi\cdot r²=\pi\cdot(\frac{diámetropizza}{2})²$

$\pi\cdot(\frac{45}{2})^2=506.25\pi$

$A=\frac{1}{8}\cdot506.25\pi$

$198.7\operatorname{cm}²$

Answer

$198.7\operatorname{cm}²$

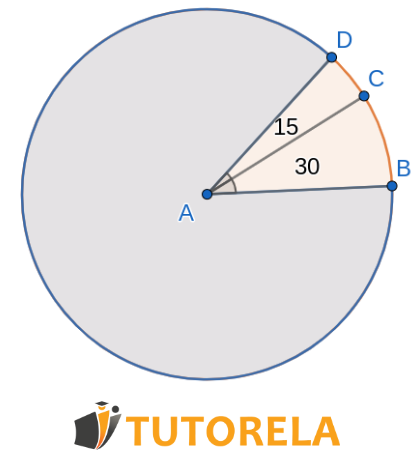
Problem

Given the circumference that at its center $O$

Is it possible to calculate its area?

Solution

The center of the circle is $O$

That is, the given line is the diameter.

Diameter = Radius multiplied by 2

$2r=10$

$r=5$

We use the formula for calculating the area

$S=\pi r^2=$

$\pi5^2=25\pi$

Answer

Yes, its area is $25\pi$

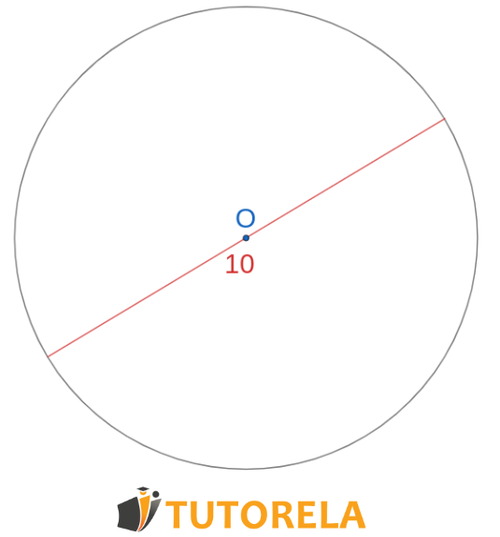
Question

Given the circle in the figure. $AB$ is the chord.

Is it possible to calculate the area of the circle?

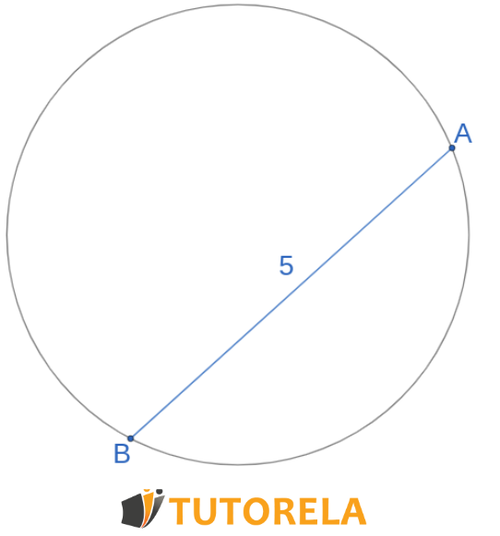
Solution

We know nothing about $AB$ other than that it is a chord we have not been given the diameter or radius, therefore it is not possible to calculate the area.

Answer

It is not possible to calculate the area

The number pi is the number of times the diameter fits in the entire circumference, in this case it fits $3.14159265358$, which is the value of $\pi$.

Different mathematicians studied the relationship between the diameter and the circumference or perimeter. Then they studied that the diameter fits $3.1415$ times in the whole circumference approximately. The way to obtain the value of pi is with the following formula:

$\frac{\text{circunferencia}}{diámetro}=\pi$

The approximate value of pi is $3.14159265358$, but to use it only 2 or 4 decimal places are enough, that is to say we can take $\pi=3.14$ or $\pi=3.1416$ if we round it up.

The number pi has an infinite number of decimal places and that is why it is considered an irrational number, but among studies of pi, 10 to 15 decimal places are usually used.