When students hear the words "compound shapes", they usually feel uncomfortable. Just before you also ask yourself: "Oh, why this again?", you should be aware that there is no real reason. Describing shapes as compound doesn't really make them so. As it turns out calculating areas and perimeters of compound shapes is in fact relatively straightforward.
How do we calculate the area of complex shapes?
How do we calculate the area of complex shapes?
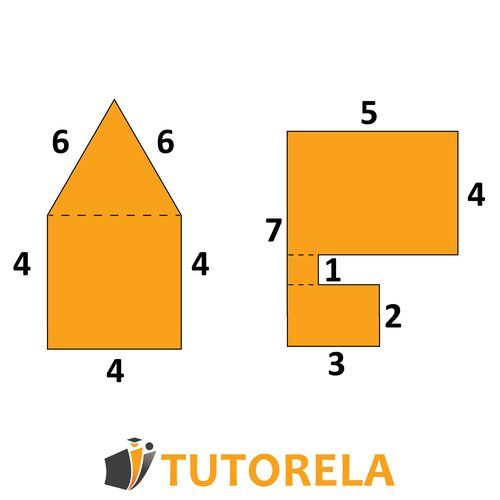
You will be introduced to Complex shapes only after you learn various shapes in geometry. The reason these shapes are complex is due to the fact that they are slightly different from those you've come to know. In each complex shape, additional shapes that you need to identify are hidden. Dividing the complex shape into several different (and familiar) shapes will allow you to answer the question of how to calculate the area of complex shapes.
The trick: extract a familiar shape from within the complex shape
So how do we answer the question of how to calculate the area of complex shapes? First, you need to identify familiar shapes within the complex shape. An example of this: a rectangle. As you know, each shape has properties that you are familiar with, so within the complex shape itself, you can apply the properties of the familiar shape and thus calculate areas and perimeters.
After completing the missing data (according to the properties of each shape, for example: rectangle), you can complete the "puzzle", identify additional data that is revealed to you, and thus calculate the area of the complex shape. When calculating the area of complex shapes, you will often need to perform simple arithmetic operations such as division and addition (mainly for sides in the shape) - all based on the unique properties of each shape.
Test yourself on area of a rectangle!
Look at the rectangle ABCD below.
Side AB is 6 cm long and side BC is 4 cm long.
What is the area of the rectangle?
How do we calculate the area of complex shapes?
When students hear the words "compound shapes", they usually feel uncomfortable. Just before you also ask yourself: "Oh, why this again?", you should know that there really is no reason. Describing shapes as compound doesn't really make them so. As it turns out calculating areas and perimeters of compound shapes can actually be relatively straightforward.
You will be introduced to Complex shapes only after you learn various shapes in geometry. The reason these shapes are complex is due to the fact that they are slightly different from those you've come to know. In each complex shape, additional shapes that you need to identify are hidden. Dividing the complex shape into several different (and familiar) shapes will allow you to answer the question of how to calculate the area of complex shapes.
The trick: extract a familiar shape from within the complex shape
So how do we answer the question of how to calculate the area of complex shapes? First, you need to identify familiar shapes within the complex shape. For example: a rectangle. As you know, each shape has properties that you are familiar with, so within the complex shape itself, you can apply the properties of the familiar shape and thus calculate areas and perimeters.
After completing the missing data (according to the properties of each shape, for example: rectangle), you can complete the "puzzle", identify additional data that becomes apparent, and thus calculate the area of the compound shape. When calculating the area of compound shapes, you will often need to perform simple arithmetic operations like division and addition (especially for sides in the shape) - all based on the unique properties of each shape.
For example: Assuming the composite shape includes several different rectangles, based on the given side lengths, it will be possible to calculate the different areas. The area of a rectangle is calculated using the formula length X width. When the side lengths are visible, subtraction and addition can be performed (according to the sizes of the rectangles and their positions within the shape) of sides, and thus calculate the area of the shape, as seen in the example below.
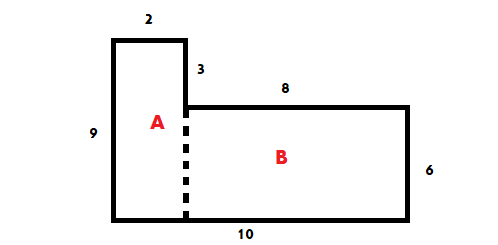
To calculate the shape's area - we will divide it in a way that creates two rectangles. We will find the area by adding and/or subtracting rectangles.
In this division we created:
A rectangle with size rectangle
A rectangle with size rectangle
The area of the entire composite shape is:
or
Look at the rectangle ABCD below.
Side AB is 4.5 cm long and side BC is 2 cm long.
What is the area of the rectangle?
Look at rectangle ABCD below.
Side AB is 10 cm long and side BC is 2.5 cm long.
What is the area of the rectangle?
The triangle ABC is given below.
AC = 10 cm
AD = 3 cm
BC = 11.6 cm
What is the area of the triangle?
Examples with solutions for Area of a Rectangle
Exercise #1
Look at the rectangle ABCD below.
Side AB is 6 cm long and side BC is 4 cm long.
What is the area of the rectangle?
Video Solution
Step-by-Step Solution
Remember that the formula for the area of a rectangle is width times height
We are given that the width of the rectangle is 6
and that the length of the rectangle is 4
Therefore we calculate:
6*4=24
Answer
24 cm²
Exercise #2
Look at the rectangle ABCD below.
Side AB is 4.5 cm long and side BC is 2 cm long.
What is the area of the rectangle?
Video Solution
Step-by-Step Solution
We begin by multiplying side AB by side BC
We then substitute the given data and we obtain the following:
Hence the area of rectangle ABCD equals 9
Answer
9 cm²
Exercise #3
Look at rectangle ABCD below.
Side AB is 10 cm long and side BC is 2.5 cm long.
What is the area of the rectangle?
Video Solution
Step-by-Step Solution
Let's begin by multiplying side AB by side BC
If we insert the known data into the above equation we should obtain the following:
Thus the area of rectangle ABCD equals 25.
Answer
25 cm²
Exercise #4
The triangle ABC is given below.
AC = 10 cm
AD = 3 cm
BC = 11.6 cm
What is the area of the triangle?
Video Solution
Step-by-Step Solution
The triangle we are looking at is the large triangle - ABC
The triangle is formed by three sides AB, BC, and CA.
Now let's remember what we need for the calculation of a triangular area:
(side x the height that descends from the side)/2
Therefore, the first thing we must find is a suitable height and side.
We are given the side AC, but there is no descending height, so it is not useful to us.
The side AB is not given,
And so we are left with the side BC, which is given.
From the side BC descends the height AD (the two form a 90-degree angle).
It can be argued that BC is also a height, but if we delve deeper it seems that CD can be a height in the triangle ADC,
and BD is a height in the triangle ADB (both are the sides of a right triangle, therefore they are the height and the side).
As we do not know if the triangle is isosceles or not, it is also not possible to know if CD=DB, or what their ratio is, and this theory fails.
Let's remember again the formula for triangular area and replace the data we have in the formula:
(side* the height that descends from the side)/2
Now we replace the existing data in this formula:
Answer
17.4
Exercise #5
What is the area of the given triangle?
Video Solution
Step-by-Step Solution
This question is a bit confusing. We need start by identifying which parts of the data are relevant to us.
Remember the formula for the area of a triangle:
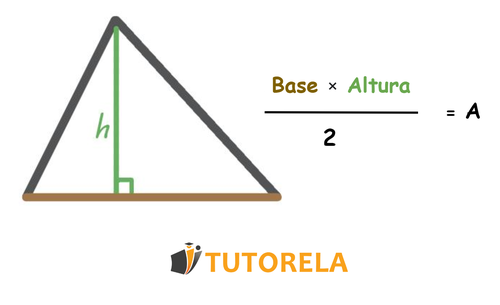 The height is a straight line that comes out of an angle and forms a right angle with the opposite side.
The height is a straight line that comes out of an angle and forms a right angle with the opposite side.
In the drawing we have a height of 6.
It goes down to the opposite side whose length is 5.
And therefore, these are the data points that we will use.
We replace in the formula:
Answer
15
More Questions
Area of a Parallelogram
Area of a Rectangle
- Rectangle Area: Solving with Width x and Length x/2 When x=4
- Calculate Rectangle Area: 3² cm Width × 1.5 cm Length
- Calculate Rectangle Area: 15 cm × 3 cm Dimensions
- Calculate Rectangle Area with Dimensions 2x and (2x-8): Variable Expression Problem
- Calculate Rectangle Area: Finding x(x-4) with Variable Dimensions
Area of a Trapezoid
- Solve for X: Trapezoid with Area 60 and Bases 8 and 14
- Calculate Trapezoid Height X: Area 30 with Bases 3.5 and 7.5
- Calculate X in Trapezoid: Given Height 5 and Base 7
- Calculate Trapezoid Area: Finding Space Between 9.6 and 13 Units
- Calculate Trapezoid Area: Finding Space with 5-Unit Top Base and 6-Unit Height
Area of a Triangle
Area of a Deltoid
- Calculate Triangle Ratios in a Deltoid: Using the 1:5 Point Relationship
- Deltoid Geometry: Calculate the 1:3 Point Division and Triangle Area Ratio
- Deltoid Area Calculation: Using 4cm and 5cm Diagonals
- Deltoid Diagonal Calculation: Finding AC When Area = 24cm² and DB = 4
- Calculate the Second Diagonal in a Deltoid with Area 18 cm² and First Diagonal 3 cm
- Area
- Trapezoids
- Symmetry in Trapezoids
- Diagonals of an isosceles trapezoid
- Area of a trapezoid
- Perimeter of a trapezoid
- Types of Trapezoids
- Isosceles Trapezoid
- Parallelogram
- The area of a parallelogram: what is it and how is it calculated?
- Perimeter of a Parallelogram
- Identifying a Parallelogram
- Rotational Symmetry in Parallelograms
- From the Quadrilateral to the Parallelogram
- Kite
- Area of a Deltoid (Kite)
- Congruent Triangles
- Parallel lines
- Angles In Parallel Lines
- Alternate angles
- Corresponding angles
- Collateral angles
- Vertically Opposite Angles
- Adjacent angles
- The Pythagorean Theorem
- Elements of the circumference
- Circle
- Diameter
- Pi
- Area of a circle
- The Circumference of a Circle
- The Center of a Circle
- Radius
- How is the radius calculated using its circumference?
- Rectangle
- From a Quadrilateral to a Rectangle
- From a Parallelogram to a Rectangle
- Calculating the Area of a Rectangle
- The perimeter of the rectangle
- Congruent Rectangles
- The sides or edges of a triangle
- Similarity of Triangles and Polygons
- Triangle similarity criteria
- Triangle Height
- Midsegment
- Midsegment of a triangle
- Midsegment of a trapezoid
- The Sum of the Interior Angles of a Triangle
- Exterior angles of a triangle
- Relationships Between Angles and Sides of the Triangle
- Relations Between The Sides of a Triangle
- Square
- Area of a square
- From Parallelogram to Square
- Rhombus, kite, or diamond?
- Diagonals of a Rhombus
- Lines of Symmetry in a Rhombus
- From Parallelogram to Rhombus
- The Area of a Rhombus
- Perimeter
- Triangle
- Types of Triangles
- Obtuse Triangle
- Equilateral triangle
- Identification of an Isosceles Triangle
- Scalene triangle
- Acute triangle
- Isosceles triangle
- The Area of a Triangle
- Area of a right triangle
- Area of Isosceles Triangles
- Area of a Scalene Triangle
- Area of Equilateral Triangles
- Perimeter of a triangle
- Cuboids
- Cubes
- How to calculate the surface area of a rectangular prism (orthohedron)
- How to calculate the volume of a rectangular prism (orthohedron)
- Lateral surface area of a rectangular prism
- Right Triangular Prism
- Bases of the Right Triangular Prism
- The lateral faces of the prism
- Lateral Edges of a Prism
- Height of a Prism
- The volume of the prism
- Surface area of triangular prisms
- Areas of Polygons for 7th Grade
- Right Triangle
- Area of a right-angled trapezoid
- Area of an isosceles trapezoid
- Corresponding exterior angles
- Alternate interior angles
- Median in a triangle
- Center of a Triangle - The Centroid - The Intersection Point of Medians
- How do we calculate the area of complex shapes?
- How to calculate the area of a triangle using trigonometry?
- How do we calculate the perimeter of polygons?
- All terms in triangle calculation
- Parts of a Circle
- Diagonals in a rectangle
- Symmetry in a kite









