Congruent Rectangles

Congruent rectangles are those that have the same area and the same perimeter. 

Let's look at an exercise as an example: 

Given the rectangles $ABCD$ and $KLMN$, as described in the following scheme:

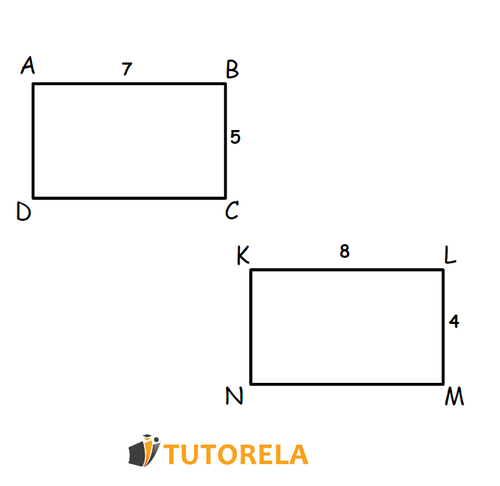
Observe the data that appears in the scheme and determine if they are congruent rectangles.

In the first rectangle we see the following: 

$AB=7$

$BC=5$

$P=24$

$A=35$

That is, the perimeter is equal to $24$ and the area, to $35$.

In the second rectangle we see the following: 

$KL=8$

$LM=4$

$P=24$

$A=32$

That is, the perimeter is equal to $24$ and the area, to $32$.

Both rectangles have the same perimeter, but their area is different.

Therefore, they are not congruent.