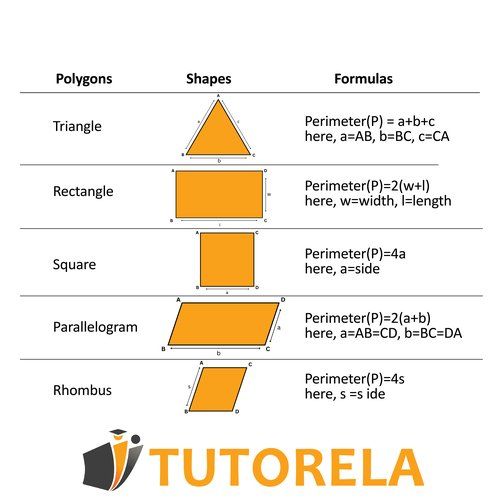
As long as we are dealing with a shape characterized by straight lines, the perimeter calculation will be performed by adding together all of the side lengths. This is a simple arithmetic operation that does not require any special skills. For example:
How do we calculate the perimeter of polygons?
How do we calculate the perimeter of polygons?
The perimeter of a shape with sides of 5, 9, 4, 6 and 7, will be 31. All you need to do is simply add up all of the sides.
Why can such a question be challenging? Owing to the fact that in tests, they don't want to examine you on arithmetic operations like addition, but rather on your proficiency in the properties of specific shapes. Therefore, you need to know the properties of polygons as they are.
Test yourself on perimeter of a triangle!
Given the parallelogram:
Calculate the perimeter of the parallelogram.
Geometry problems require you to answer various questions:
- What is the perimeter of a shape.
- Calculating the area of a shape.
- Finding the length of a side and more...
How do we calculate the perimeter of polygons?
As long as we are dealing with a shape characterized by straight lines, the perimeter calculation will be performed by adding together all of the side lengths. This is a simple arithmetic operation that does not require any special skills. For example:
The perimeter of a shape with sides of 5, 9, 4, 6 and 7, will be 31. All you need to do is add up all the sides.
Why can such a question be challenging? Owing to the fact that in tests, they don't want to examine you on arithmetic operations like addition, but rather on your proficiency in the properties of specific shapes. Therefore, you need to know the properties of polygons as they are.
Example: Calculating the perimeter of a parallelogram
For example, you may encounter a question as seen below.
Given a parallelogram with sides of 5 and 6, determine the perimeter of the parallelogram.
In order to correctly answer this question, you need to know the properties of a parallelogram. We know that parallel sides in a parallelogram are equal, thus you can conclude that the length of the other sides are 5 and 8. Therefore, the perimeter of the parallelogram in this case will be 26 (5 + 8 + 5 + 8).
Additional examples:
Question: Given an isosceles triangle with a perimeter of 48. Leg a = 12. Determine the value of the base?
Answer: Given that this is an isosceles triangle, leg b is also equal to 12. Therefore, the base equals 24. (12+12 = 24)
Question: Given an isosceles triangle with a base of 26. The length of side a is 8. What is the perimeter of the triangle?
Answer: Since the triangle is isosceles, side b is also equal to 8. Therefore, the perimeter is 8 + 8 + 26 = 42.
Question: Given an equilateral triangle with side a equal to 9. What is the perimeter of the triangle?
Answer: Since the triangle is equilateral, all sides are equal. Therefore, the perimeter of the triangle is 27.
Question: Given a rectangle with adjacent sides of length 7 and 9. Determine the perimeter of the rectangle?
Answer: Since in a rectangle opposite sides are equal, we can conclude that the other sides are equal to 7 and 9. Therefore, the perimeter of the rectangle is 32.
Join Over 30,000 Students Excelling in Math!
Endless Practice, Expert Guidance - Elevate Your Math Skills Today
Test your knowledge
Question 1
Find the perimeter of the triangle ABC
Question 2
Look at the rectangle below.
Side AB is 2 cm long and side BC has a length of 7 cm.
What is the perimeter of the rectangle?
Question 3
Look at the following rectangle:
Find its perimeter.
Examples with solutions for Perimeter of a Triangle
Exercise #1
Given the parallelogram:
Calculate the perimeter of the parallelogram.
Video Solution
Step-by-Step Solution
To find the perimeter of the parallelogram, we follow these steps:
- Step 1: Identify the given side lengths from the diagram: units and units.
- Step 2: Use the perimeter formula for a parallelogram, which is .
- Step 3: Substituting the given values into the formula: and .
Proceeding with the calculation:
.
Therefore, the perimeter of the parallelogram is 12 units.
Answer
12
Exercise #2
Find the perimeter of the triangle ABC
Video Solution
Step-by-Step Solution
To find the perimeter of triangle , we need to sum the lengths of its sides:
- Side
- Side
- Side
Using the formula for the perimeter of a triangle:
Substitute the known values:
Thus, the perimeter of triangle is .
From the multiple-choice options provided, the correct choice is option 1: 12.
Answer
12
Exercise #3
Look at the rectangle below.
Side AB is 2 cm long and side BC has a length of 7 cm.
What is the perimeter of the rectangle?
Video Solution
Step-by-Step Solution
Given that in a rectangle every pair of opposite sides are equal to each other, we can state that:
Now we can add all the sides together and find the perimeter:
Answer
18 cm
Exercise #4
Look at the following rectangle:
Find its perimeter.
Video Solution
Step-by-Step Solution
Since in a rectangle all pairs of opposite sides are equal:
Now we calculate the perimeter of the rectangle by adding the sides:
Answer
28
Exercise #5
Look at the trapezoid in the figure.
Calculate its perimeter.
Video Solution
Step-by-Step Solution
To solve this problem, we'll follow these steps:
- Step 1: Identify all given side lengths of the trapezoid.
- Step 2: Apply the formula for the perimeter of the trapezoid.
- Step 3: Sum up the lengths to find the perimeter.
Now, let's work through each step:
Step 1: The problem gives us the lengths of the trapezoid's sides:
-
-
-
-
Step 2: We use the formula for the perimeter of a trapezoid:
Step 3: Plugging in the given values, we calculate:
Calculating further, we have:
Therefore, the perimeter of the trapezoid is .
Answer
24.2
More Questions
Perimeter of a Rectangle
- Calculate Rectangle Perimeter: Finding the Total Length of a 4.8 cm × 12 cm Rectangle
- Calculate the Perimeter: Finding Border Length in a 2×4×5 Rectangular Diagram
- Calculate Parallelogram Area: Rectangle with Perimeter 24 Inside
- Calculate the Perimeter: Rectangle Composed of Two Equal Squares
- Calculate Rectangle Area: Given Perimeter 30cm and Height 5cm
Perimeter of a Parallelogram
- Calculate Parallelogram Area: 38cm Perimeter with Proportional Sides
- Calculate Parallelogram Height: Area 24 cm², Perimeter 24 cm with Double-Length Side
- Calculate Parallelogram Area: 22cm Perimeter with 2cm Height
- Calculate Parallelogram Area: 22cm Perimeter with 3cm Height
- Parallelogram Side Length: Finding Missing Side Given 9cm and 30cm Perimeter
Perimeter of a Trapezoid
- Calculate Trapezoid Perimeter: Inside an Isosceles Triangle with Height 8
- Calculate Trapezoid Perimeters: Comparing Two Shapes with 7-Unit Parallel Sides
- Calculate Trapezoid Perimeter: Finding the Sum of Sides 4, 5, 6, and 9
- Compare Two Trapezoids: Analyzing Measurements x+5, 17, and Variable y
- Calculate the Perimeter of an Isosceles Trapezoid with Sides 3, 5, and 7
Perimeter of a Triangle
- Calculate Triangle Perimeter: Finding the Sum of Sides 6, 8, and 10
- Calculate the Perimeter of an Equilateral Triangle with 5-Unit Sides
- Find X in an Equilateral Triangle with 33cm Perimeter
- Calculate the Perimeter: Isosceles Triangle with Sides 6 and Base 4
- Solve for X: Finding the Side Length in an Isosceles Triangle with Perimeter 50
Related Subjects
- Area
- Trapezoids
- Symmetry in Trapezoids
- Diagonals of an isosceles trapezoid
- Area of a trapezoid
- Perimeter of a trapezoid
- Types of Trapezoids
- Isosceles Trapezoid
- Parallelogram
- The area of a parallelogram: what is it and how is it calculated?
- Perimeter of a Parallelogram
- Identifying a Parallelogram
- Rotational Symmetry in Parallelograms
- From the Quadrilateral to the Parallelogram
- Kite
- Area of a Deltoid (Kite)
- Congruent Triangles
- Parallel lines
- Angles In Parallel Lines
- Alternate angles
- Corresponding angles
- Collateral angles
- Vertically Opposite Angles
- Adjacent angles
- The Pythagorean Theorem
- Elements of the circumference
- Circle
- Diameter
- Pi
- Area of a circle
- The Circumference of a Circle
- The Center of a Circle
- Radius
- How is the radius calculated using its circumference?
- Rectangle
- From a Quadrilateral to a Rectangle
- From a Parallelogram to a Rectangle
- Calculating the Area of a Rectangle
- The perimeter of the rectangle
- Congruent Rectangles
- The sides or edges of a triangle
- Similarity of Triangles and Polygons
- Triangle similarity criteria
- Triangle Height
- Midsegment
- Midsegment of a triangle
- Midsegment of a trapezoid
- The Sum of the Interior Angles of a Triangle
- Exterior angles of a triangle
- Relationships Between Angles and Sides of the Triangle
- Relations Between The Sides of a Triangle
- Square
- Area of a square
- From Parallelogram to Square
- Rhombus, kite, or diamond?
- The Area of a Rhombus
- Perimeter
- Triangle
- Types of Triangles
- Obtuse Triangle
- Equilateral triangle
- Identification of an Isosceles Triangle
- Scalene triangle
- Acute triangle
- Isosceles triangle
- The Area of a Triangle
- Area of a right triangle
- Area of Isosceles Triangles
- Area of a Scalene Triangle
- Area of Equilateral Triangles
- Perimeter of a triangle
- Cuboids
- Cubes
- How to calculate the surface area of a rectangular prism (orthohedron)
- How to calculate the volume of a rectangular prism (orthohedron)
- Lateral surface area of a rectangular prism
- Right Triangular Prism
- Bases of the Right Triangular Prism
- The lateral faces of the prism
- Lateral Edges of a Prism
- Height of a Prism
- The volume of the prism
- Surface area of triangular prisms
- Areas of Polygons for 7th Grade
- Right Triangle
- Area of a right-angled trapezoid
- Area of an isosceles trapezoid
- Corresponding exterior angles
- Alternate interior angles
- Median in a triangle
- Center of a Triangle - The Centroid - The Intersection Point of Medians
- How do we calculate the area of complex shapes?
- How to calculate the area of a triangle using trigonometry?
- How do we calculate the perimeter of polygons?
- All terms in triangle calculation
- Parts of a Circle
- Diagonals in a rectangle
