A polygon defines a geometric shape that is made up of sides. In other words, under the umbrella of polygons fall the following square, rectangle, parallelogram, trapezoid, and many more.
Areas of Polygons for 7th Grade
Areas of Polygons
Polygon Definition
For example, a triangle has 3 sides, every quadrilateral has 4 sides, and so on.
We have already learned to calculate the areas of standard polygons. There are also non-standard polygons, for which there is no specific formula. However, their area of complex shapes can be calculated using two methods:
- We can divide the area of the required polygon into several areas of polygons that we are familiar with, calculate the areas separately, and then add them together to obtain the final area.
- We can try to "complete" the area of the required polygon into another polygon whose area we know how to calculate, and the proceed to subtract the area we added. This way, we can obtain the area of the original polygon.
Example
Let's demonstrate this using a simple exercise:
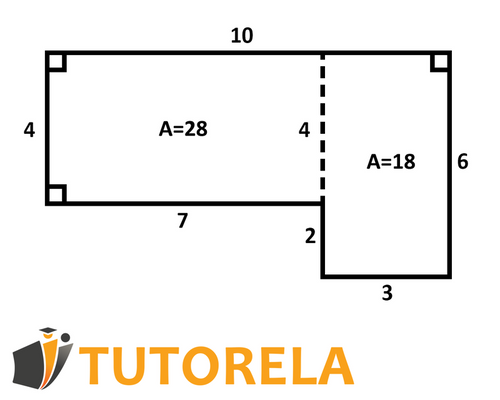
Here is a drawing of a polygon.
We need to calculate its area. From the start, we can see that this is not a standard polygon, so we will use the first method to calculate its area. We will divide the polygon as shown in the drawing, and we should obtain two rectangles.
According to the data shown in the drawing, in the rectangle on the right side we obtain the side lengths of 3 and 6, therefore the area of the rectangle will be 18 (multiplication of the two values). In the rectangle on the left side we obtain the side lengths of 4 and 7, therefore the area of the rectangle will be 28 (multiplication of the two values). Thus, the total area of the polygon will be the sum of the two areas we calculated separately, meaning, 18+28=46.
Test yourself on area of a rectangle!
Complete the sentence:
To find the area of a right triangle, one must multiply ________________ by each other and divide by 2.
In 7th grade we focus on learning about several polygons (click on the links for in-depth reading):
How to calculate areas of polygons
The formula for calculating the area of a polygon varies according to the polygon in question. (Click on the titles to read the full articles including examples and practice)
A parallelogram has a length equal to 6 cm and a height equal to 4.5 cm.
Calculate the area of the parallelogram.
Look at the rectangle ABCD below.
Side AB is 6 cm long and side BC is 4 cm long.
What is the area of the rectangle?
Calculate the area of the following triangle:
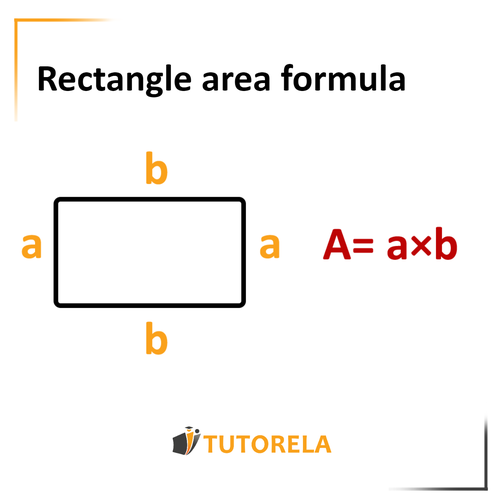
Calculating Rectangle Area
The formula for calculating the area of a rectangle is: width X length.
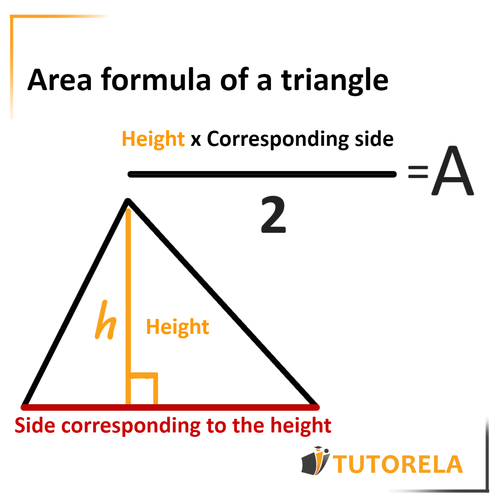
Calculating the area of any triangle
The formula for calculating the area of any triangle: base X height divided by 2
Calculate the area of the following triangle:
Calculate the area of the triangle using the data in the figure below.
AB = 5 cm
The height of the rectangle is 2 cm.
Calculate the area of the parallelogram.
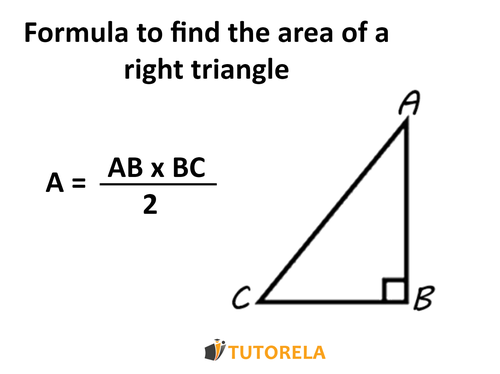
Calculating the area of a right triangle
In the case of a right triangle's area, it's the same formula, but the height is actually one of the sides
Calculating the Area of a Parallelogram
The area of a parallelogram is calculated by multiplying one of its sides by the height.
For example in the drawing, you can calculate the area of the parallelogram by multiplying DC by h1 and then dividing by 2, or by multiplying BC by h2 and then dividing by 2
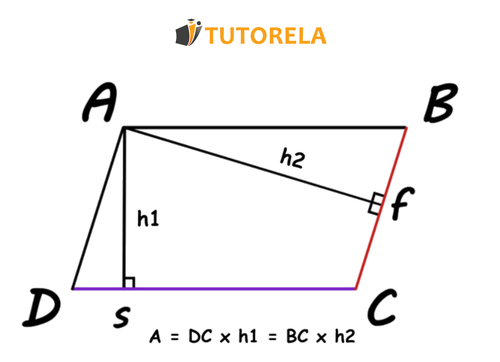
Given the following trapezoid:
Calculate the area of the trapezoid ABCD.
Given the following rectangle:
Find the area of the rectangle.
AB = 6 cm
The height of the rectangle is 2 cm.
Calculate the area of the parallelogram.
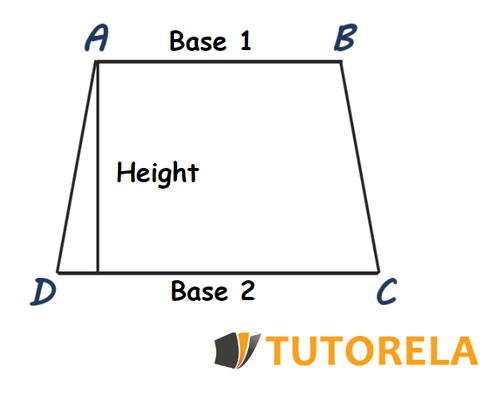
Calculating the Area of a Trapezoid
The formula for calculating the area of a trapezoid is the sum of the two bases X the height divided by 2
AB = 17 cm
The height of the rectangle is 8 cm.
Calculate the area of the parallelogram.
Look at the rectangle ABCD below.
Side AB is 4.5 cm long and side BC is 2 cm long.
What is the area of the rectangle?
Given the trapezoid:
What is the area?
Examples with solutions for Areas of Polygons for 7th Grade
Exercise #1
Complete the sentence:
To find the area of a right triangle, one must multiply ________________ by each other and divide by 2.
Step-by-Step Solution
To solve this problem, begin by identifying the elements involved in calculating the area of a right triangle. In a right triangle, the two sides that form the right angle are known as the legs. These legs act as the base and height of the triangle.
The formula for the area of a triangle is given by:
In the case of a right triangle, the base and height are the two legs. Therefore, the process of finding the area involves multiplying the lengths of the two legs together and then dividing the product by 2.
Based on this analysis, the correct way to complete the sentence in the problem is:
To find the area of a right triangle, one must multiply the two legs by each other and divide by 2.
Answer
the two legs
Exercise #2
A parallelogram has a length equal to 6 cm and a height equal to 4.5 cm.
Calculate the area of the parallelogram.
Video Solution
Step-by-Step Solution
To solve this problem, let's apply the formula for the area of a parallelogram:
The formula for the area of a parallelogram is .
Here, the base of the parallelogram is 6 cm, and the height is 4.5 cm.
Substituting these values into the formula gives:
Performing the multiplication:
square centimeters.
Therefore, the area of the parallelogram is .
Referring to the given multiple-choice answers, the correct choice is:
Choice 3: .
Answer
27
Exercise #3
Look at the rectangle ABCD below.
Side AB is 6 cm long and side BC is 4 cm long.
What is the area of the rectangle?
Video Solution
Step-by-Step Solution
Remember that the formula for the area of a rectangle is width times height
We are given that the width of the rectangle is 6
and that the length of the rectangle is 4
Therefore we calculate:
6*4=24
Answer
24 cm²
Exercise #4
Calculate the area of the following triangle:
Video Solution
Step-by-Step Solution
The formula for calculating the area of a triangle is:
(the side * the height from the side down to the base) /2
That is:
We insert the existing data as shown below:
Answer
10
Exercise #5
Calculate the area of the triangle using the data in the figure below.
Video Solution
Step-by-Step Solution
To solve the problem of finding the area of triangle , we follow these steps:
- Step 1: Identify the given measurements.
- Step 2: Use the appropriate formula for the area of a triangle.
- Step 3: Calculate the area using these measurements.
Let's go through each step in detail:
Step 1: From the figure, the base and height .
Step 2: The formula for the area of a triangle is: .
Step 3: Substituting the known values into the formula, we get:
Therefore, the area of triangle is 10.
Answer
10
More Questions
Area of a Triangle
Area of a Parallelogram
Area of a Rectangle
- Rectangle Area: Solving with Width x and Length x/2 When x=4
- Calculate Rectangle Area: 3² cm Width × 1.5 cm Length
- Calculate Rectangle Area: 15 cm × 3 cm Dimensions
- Calculate Rectangle Area with Dimensions 2x and (2x-8): Variable Expression Problem
- Calculate Rectangle Area: Finding x(x-4) with Variable Dimensions
Area of a Trapezoid
- Solve for X: Trapezoid with Area 60 and Bases 8 and 14
- Calculate Trapezoid Height X: Area 30 with Bases 3.5 and 7.5
- Calculate X in Trapezoid: Given Height 5 and Base 7
- Calculate Trapezoid Area: Finding Space Between 9.6 and 13 Units
- Calculate Trapezoid Area: Finding Space with 5-Unit Top Base and 6-Unit Height
- Area
- Trapezoids
- Symmetry in Trapezoids
- Diagonals of an isosceles trapezoid
- Area of a trapezoid
- Perimeter of a trapezoid
- Types of Trapezoids
- Isosceles Trapezoid
- Parallelogram
- The area of a parallelogram: what is it and how is it calculated?
- Perimeter of a Parallelogram
- Identifying a Parallelogram
- Rotational Symmetry in Parallelograms
- From the Quadrilateral to the Parallelogram
- Kite
- Area of a Deltoid (Kite)
- Congruent Triangles
- Parallel lines
- Angles In Parallel Lines
- Alternate angles
- Corresponding angles
- Collateral angles
- Vertically Opposite Angles
- Adjacent angles
- The Pythagorean Theorem
- Elements of the circumference
- Circle
- Diameter
- Pi
- Area of a circle
- The Circumference of a Circle
- The Center of a Circle
- Radius
- How is the radius calculated using its circumference?
- Rectangle
- From a Quadrilateral to a Rectangle
- From a Parallelogram to a Rectangle
- Calculating the Area of a Rectangle
- The perimeter of the rectangle
- Congruent Rectangles
- The sides or edges of a triangle
- Similarity of Triangles and Polygons
- Triangle similarity criteria
- Triangle Height
- Midsegment
- Midsegment of a triangle
- Midsegment of a trapezoid
- The Sum of the Interior Angles of a Triangle
- Exterior angles of a triangle
- Relationships Between Angles and Sides of the Triangle
- Relations Between The Sides of a Triangle
- Square
- Area of a square
- From Parallelogram to Square
- Rhombus, kite, or diamond?
- The Area of a Rhombus
- Perimeter
- Triangle
- Types of Triangles
- Obtuse Triangle
- Equilateral triangle
- Identification of an Isosceles Triangle
- Scalene triangle
- Acute triangle
- Isosceles triangle
- The Area of a Triangle
- Area of a right triangle
- Area of Isosceles Triangles
- Area of a Scalene Triangle
- Area of Equilateral Triangles
- Perimeter of a triangle
- Cuboids
- Cubes
- How to calculate the surface area of a rectangular prism (orthohedron)
- How to calculate the volume of a rectangular prism (orthohedron)
- Lateral surface area of a rectangular prism
- Right Triangular Prism
- Bases of the Right Triangular Prism
- The lateral faces of the prism
- Lateral Edges of a Prism
- Height of a Prism
- The volume of the prism
- Surface area of triangular prisms
- Areas of Polygons for 7th Grade
- Right Triangle
- Area of a right-angled trapezoid
- Area of an isosceles trapezoid
- Corresponding exterior angles
- Alternate interior angles
- Median in a triangle
- Center of a Triangle - The Centroid - The Intersection Point of Medians
- How do we calculate the area of complex shapes?
- How to calculate the area of a triangle using trigonometry?
- How do we calculate the perimeter of polygons?
- All terms in triangle calculation
- Parts of a Circle
- Diagonals in a rectangle









