Calculate the lengths of all possible diagonals on the faces of the rectangular prism below: 4 4 4 7 7 7 5 5 5

$$ \sqrt{74},\sqrt{41},\sqrt{65} $$

$$ \sqrt{74},\sqrt{24},\sqrt{65} $$

Given the cuboid whose length is equal to 9 cm Width is equal to 3 cm Side AB equals 10 cm Is it possible to calculate the volume of the cuboid? 9 9 9 3 3 3 10 10 10 A A A B B B

You can, $$ 36\cdot\sqrt{19} $$ cm³

The Application of the Pythagorean Theorem to an Orthohedron or Cuboid

Pythagorean Theorem in an Orthohedron

The orthohedron or cuboid is a rectangular prism, a three-dimensional figure, that is, it has length, width, and height (or depth). In addition, the angles between the different planes are right angles, which allows us to make use of the Pythagorean theorem to calculate the length of different sections of the orthohedron.

Reminder of the Pythagorean theorem:

The Pythagorean theorem states that in a right-angled triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides. Basiclly:
$a²+b² = c²$
This principle can be extended to three-dimensional shapes like cuboids or orthohedrons.

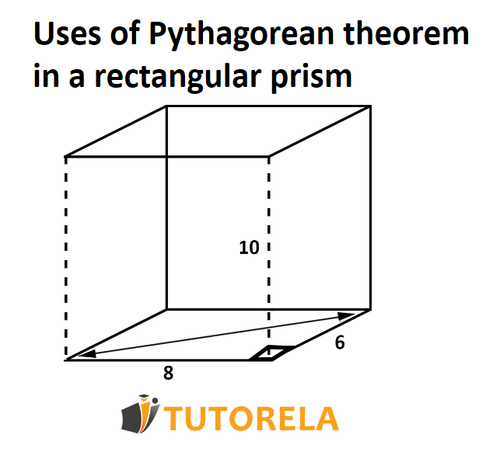
A1- Uses of the Pythagorean theorem in an orthohedron

The Space Diagonal

The Pythagorean theorem can help find the length of the diagonals on the faces of an orthohedron, but it also extends to finding the space diagonal—the diagonal that runs through the interior of a cuboid from one corner to its opposite corner.

There are two methods to find this:

Use the Pythagorean theorem twice: First, find one face diagonal, then use it to calculate the space diagonal.
Use the formula:
$d=l^2+w^2+h^2$
where $I$ , $w$ , and $h$ are the length, width, and height of the cuboid, respectively.

Detailed explanation

Start practice

Test yourself on using the pythagorean theorem in cuboids!

Look at the orthohedron in the figure below.

Which angle is between the diagonal BH and the face ABFE?

Practice more now

We will illustrate this with an example.

Given an orthohedron as represented in the diagram.

The dimensions of the box are $6$ , $8$ and $10$ .

We are asked to calculate the dimensions of the diagonal of the lower base of the box.

We will look at the diagram and see that the base of the box is, in fact, a rectangle whose edges measure $6$ and $8$ . These edges also serve as legs with a right angle between them.

Therefore, we will use the Pythagorean theorem and calculate the hypotenuse which, in fact, is the required diagonal.

According to the Pythagorean theorem we will obtain:

$X=10$

That is, the diagonal measures $10$ .