Lines of Symmetry in a Rhombus

Before we talk about the symmetry of a rhombus, let's remember that we have two types of symmetry. Mirror symmetry and rotational symmetry.

A figure with mirror symmetry is a figure that, when folded and divided vertically into two parts by the central axis, its halves would match exactly.

A figure with rotational symmetry is a figure that "hides", coincides with itself, more than once, when making a complete rotation.

The rhombus has mirror symmetry and also rotational symmetry.

The axis of symmetry of the rhombus passes through every pair of opposite angles.

As we well know,

if we can draw a vertical line and fold the figure along it to obtain two parts that will merge with each other, the figure is considered symmetrical.

We can cross the rhombus with axes of symmetry through each pair of opposite angles.

Let's draw a vertical line of symmetry through a pair of opposite angles and we can clearly see that two sections are created and, when we fold the diamond along this axis, the sections join exactly one with the other.

A great way to demonstrate this is through the congruence of the two triangles that were created by the SSS congruence theorem.

In the diamond, all sides are equal and the line of symmetry is a common side.

Let's remember that the order of symmetry is the number of times that all parts of a certain figure coincide when making a full turn.

Let's see it in the illustration:

If we rotate it a quarter turn, it still won't match.

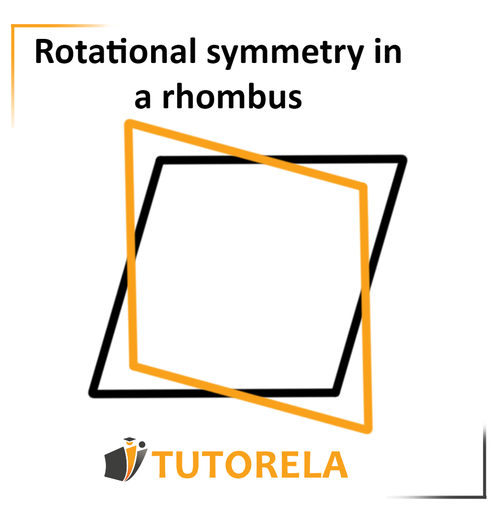
Now, let's rotate it another quarter turn,

that is, we have now made a half turn, and let's see how all its parts match, it is covered.

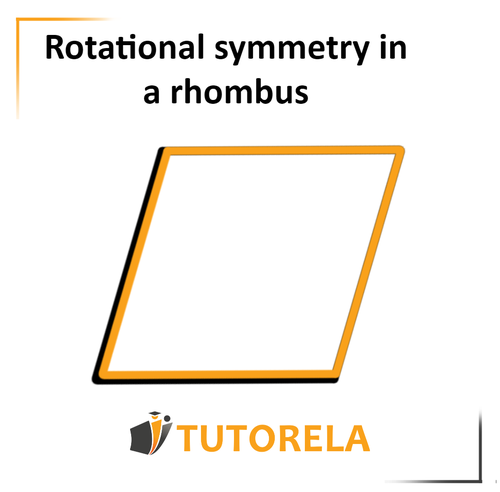
At this stage, we can determine that the rhombus has rotational symmetry. It has not yet made a full turn and there was already a match.

Let's now continue to the full turn to discover the order of symmetry of the rhombus.

If we keep rotating it another quarter turn, the rhombus will not match.

If we keep rotating it another quarter turn, in fact, we will have made a full turn, the rhombus will again be covered, it will match its original shape, and this will be the second time it does so in a turn.

Therefore, we can determine that the rhombus has second-order rotational symmetry.