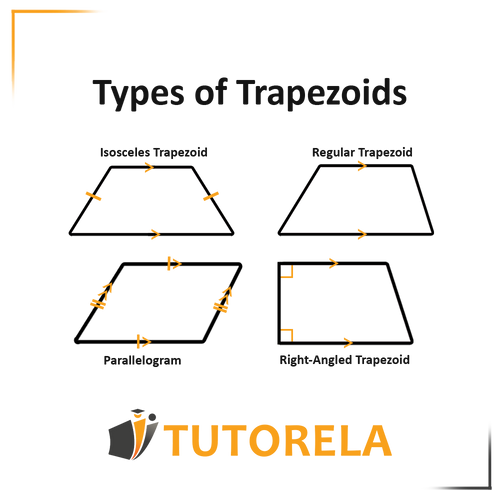
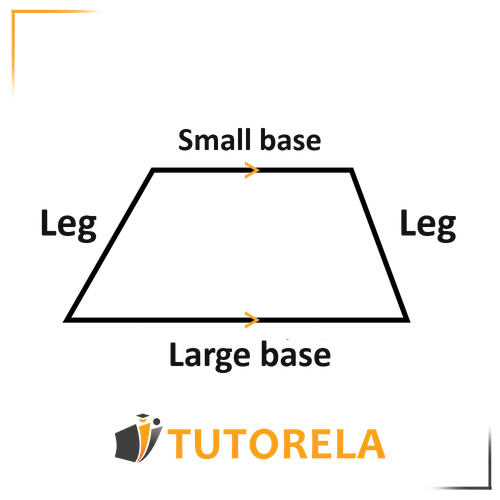
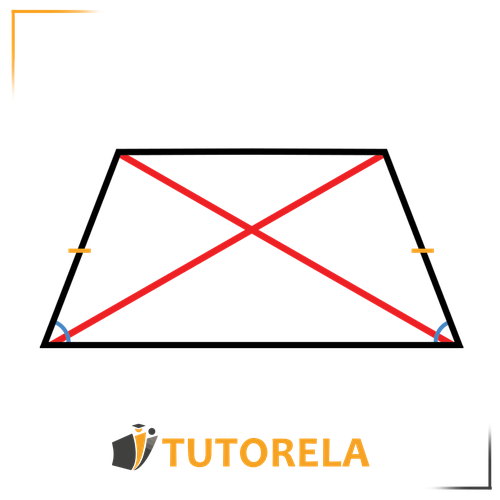
Given that the trapezoid is isosceles and the angles on both sides are equal, it can be argued that:
∢C=∢D
∢A=∢B
We know that the sum of the angles of a quadrilateral is 360 degrees.
Therefore we can create the formula:
∢A+∢B+∢C+∢D=360
We replace according to the existing data:
120+120+2x+2x=360
240+4x=360
4x=360−240
4x=120
We divide the two sections by 4:
44x=4120
x=30