In an isosceles trapezoid, there is mirror symmetry.
A shape with mirror symmetry is a shape that is divided by the vertical line of symmetry into two parts that will join if we fold one on top of the other.
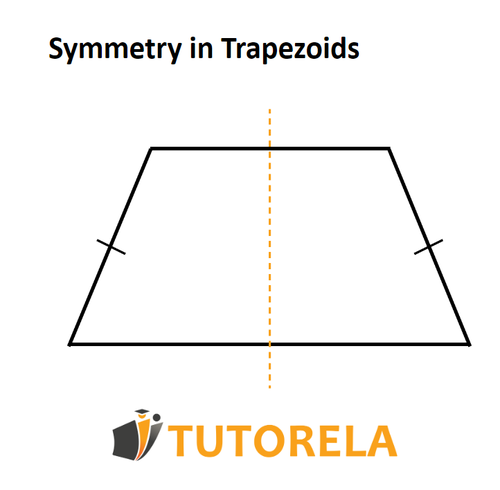
In an isosceles trapezoid, there is mirror symmetry.
A shape with mirror symmetry is a shape that is divided by the vertical line of symmetry into two parts that will join if we fold one on top of the other.

Before talking about what symmetry in a trapezoid is and whether it exists, first we will understand what symmetry is in general and under what conditions a shape is called symmetrical.
There are several types of symmetry, including rotational symmetry and mirror symmetry.
In this article, we will only talk about mirror symmetry.
If we can draw a vertical folding line in some way, fold the shape along it and obtain two parts that will merge into each other, the shape will be called a symmetrical shape.
The folding line will be called the line of symmetry of the shape.
Do you have any questions?
The dashed orange line will be the folding line, the line of symmetry.
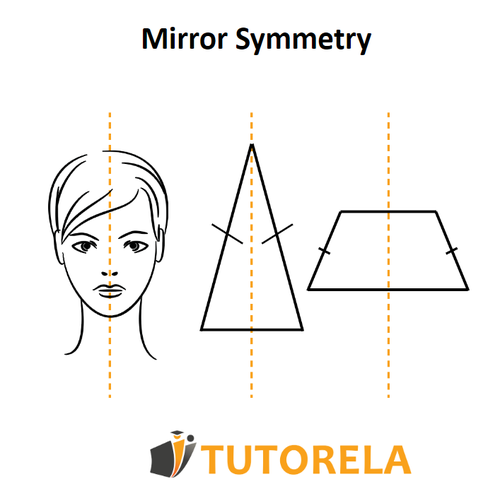
Now imagine that we fold the two parts created by the folding line inward, one on top of the other.
We can see that in all the previous shapes, the two parts have merged so that these shapes have a transparent symmetry.
How do we remember it?
In the mirror reflection, you see exactly what appears in reality.
So also in mirror symmetry, one part of the shape is perfectly reflected with the other part.
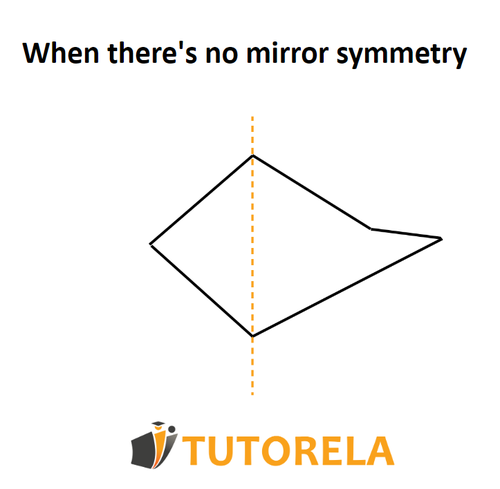
If we fold the two parts onto each other, they will not join and, therefore, there is no mirror symmetry in this way.
Now that we understand what symmetry is, we can determine that in an isosceles trapezoid there is a mirror symmetry.
Let's understand this:
In front of us, there is an isosceles trapezoid.
We will pass a vertical axis of symmetry right in the middle of the trapezoid:
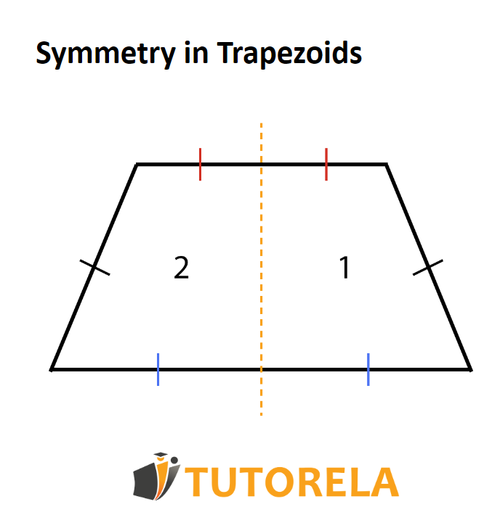
The axis of symmetry cuts the top and bottom base of the trapezoid in half.
Therefore, now we have on one side
A shape that consists of:
and a second shape that consists of:
Since the edges are equal and half is equal to half, we can determine that the two parts created by the axis of symmetry merge (if you fold one on top of the other) and therefore, in an isosceles trapezoid there is a mirror symmetry.
What happens with a non-isosceles trapezoid?
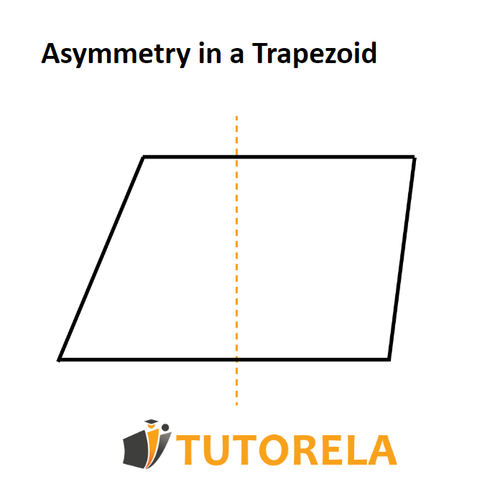
And draw a vertical line of symmetry for it.
We can clearly see that the axis of symmetry does not pass through the mid-base and does not divide this common trapezoid into two parts that will merge if we fold them.