The Parabola
This function is a quadratic function and is called a parabola.
We will focus on two main types of parabolas: maximum and minimum parabolas.
Master quadratic functions with step-by-step practice problems. Learn to find parabola vertex, identify maximum/minimum, and determine domains of increase.
This function is a quadratic function and is called a parabola.
We will focus on two main types of parabolas: maximum and minimum parabolas.
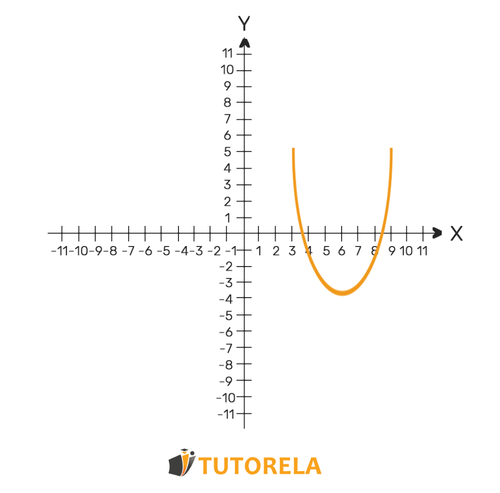
Also called smiling or happy.
A vertex is the minimum point of the function, where is the lowest.
We can identify that it is a minimum parabola if the equation is positive.
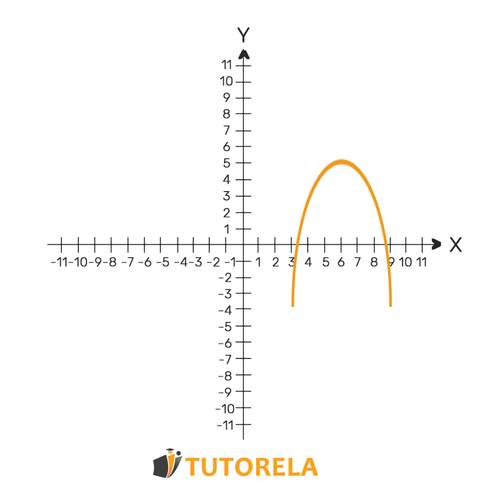
Also called sad or crying.
A vertex is the maximum point of the function, where is the highest.
We can identify that it is a maximum parabola if the equation is negative.
To the parabola,
the vertex marks its highest point.
How do we find it?
Identify the coefficients based on the following equation
\( y=x^2 \)
Determine the value of the coefficient in the following equation:
The quadratic equation in the problem is already arranged (meaning all terms are on one side and 0 on the other side), so let's proceed to answer the question asked:
The question asked in the problem - What is the value of the coefficient in the equation?
Let's recall the definitions of coefficients in solving quadratic equations and the roots formula:
The rule states that the roots of an equation of the form:
are:
That is the coefficient is the coefficient of the quadratic term (meaning the term with the second power)- Let's examine the equation in the problem:
Remember that the minus sign before the quadratic term means multiplication by: , therefore- we can write the equation as:
The number that multiplies the , is hence we identify that the coefficient of the quadratic term is the number ,
Therefore the correct answer is A.
Answer:
-1
Identify the coefficients based on the following equation
Let's determine the coefficients for the quadratic function given by .
Comparing these coefficients to the provided choices, the correct answer is:
.
Therefore, the correct choice is Choice 4.
Answer:
Identify the coefficients based on the following equation
To solve this problem, we'll follow these steps:
Now, let's work through each step:
Step 1: The given quadratic function is .
Step 2: The standard form of a quadratic equation is .
Step 3: By matching the given quadratic function with the standard form:
- The coefficient of is , so .
- The coefficient of is , so .
- The constant term is , so .
Therefore, the solution to the problem is , , .
Answer:
Identify the coefficients based on the following equation
To solve this problem, we'll follow these steps:
Now, let's work through each step:
Step 1: The given quadratic function is . The standard form for a quadratic equation is .
Step 2: By comparing the given equation to the standard form, we can identify the coefficients:
- , from the term .
- , from the term .
- , from the constant term .
Step 3: With these values, compare them to the given choices. The choice that matches these values is option 3: .
Therefore, the solution to the problem is .
Answer:
Identify the coefficients based on the following equation
To solve this problem, we will follow these steps:
Now, let's work through each step:
Step 1: The standard form of a quadratic function is .
Step 2: Given the function , we compare this with the standard form:
Therefore, the solution to the problem is .
Answer: