Axis of Symmetry Practice Problems and Solutions

To determine the symmetry (vertex) point of the quadratic function $f(x) = \frac{1}{2}x^2$, we will use the formula for the x-coordinate of the vertex (or axis of symmetry) for a general quadratic function $f(x) = ax^2 + bx + c$, which is given by:

• $x = -\frac{b}{2a}$

In this problem, the coefficients are $a = \frac{1}{2}$, $b = 0$, and $c = 0$. By substituting these values into the vertex formula:

$x = -\frac{0}{2 \times \frac{1}{2}} = 0$

This tells us that the x-coordinate of the vertex is $0$. To find the y-coordinate of the vertex, we substitute $x = 0$ back into the function $f(x) = \frac{1}{2}(x^2)$:

$f(0) = \frac{1}{2}(0)^2 = 0$

Thus, the vertex of the function, also its symmetry point, is at the coordinate $(0,0)$.

Therefore, the symmetry point of the function $f(x) = \frac{1}{2}x^2$ is $(0, 0)$.

To find the axis of symmetry for the quadratic function $f(x) = -3x^2 + 3$, we follow these steps:

• Identify coefficients: Here, $a = -3$, $b = 0$, and $c = 3$.
• Use the axis of symmetry formula for a quadratic $ax^2 + bx + c$ given by $x = -\frac{b}{2a}$.
• Substitute $b = 0$ and $a = -3$ into the formula: $x = -\frac{0}{2 \times (-3)}$.
• This simplifies to $x = 0$.

The axis of symmetry for the quadratic function $f(x) = -3x^2 + 3$ is therefore $x = 0$.

To solve this problem, we'll follow these steps:

• Identify the coefficients of the quadratic function.
• Apply the vertex formula to find the axis of symmetry and subsequently the vertex.
• Calculate the function's value at the symmetry point.

Now, let's work through each step:
Step 1: The given function is $f(x) = 2x^2$, where $a = 2$ and $b = 0$.
Step 2: The axis of symmetry for a quadratic function in the form $ax^2 + bx + c$ is given by $x = -\frac{b}{2a}$. With $b = 0$, this simplifies to $x = 0$.
Step 3: To find the vertex, calculate the function's value at $x = 0$, using $f(x) = 2x^2$.
Plugging in $x = 0$, we find:
$f(0) = 2(0)^2 = 0$.
Thus, the vertex, and hence the symmetry point of the function, is $(0, 0)$.

Therefore, the solution to the problem is $(0, 0)$.

To solve this problem, we'll follow these steps:

• Step 1: Identify the coefficients in the quadratic equation.
• Step 2: Apply the formula for the axis of symmetry.
• Step 3: Substitute the coefficients into the formula and solve.

Now, let's work through each step:
Step 1: The quadratic function given is $f(x) = 7x^2$ which can be written in the form $ax^2 + bx + c$. Here, $a = 7$, $b = 0$, and $c = 0$.
Step 2: We'll use the formula for the axis of symmetry: $x = -\frac{b}{2a}$.
Step 3: Substitute $a = 7$ and $b = 0$ in the formula:
$x = -\frac{0}{2 \times 7} = 0$ Therefore, the axis of symmetry for the quadratic function $f(x) = 7x^2$ is $x = 0$.

Therefore, the solution to the problem is $x = 0$, corresponding to choice #3.

To solve this problem, we'll follow these steps:

• Step 1: Identify the coefficients $a$, $b$, and $c$ from the quadratic function.
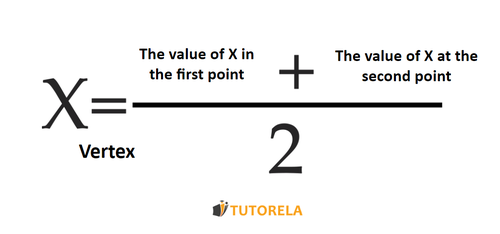
• Step 2: Apply the vertex formula to find the x-coordinate of the symmetry point.
• Step 3: Substitute the x-coordinate back into $f(x)$ to find the y-coordinate of the vertex.
• Step 4: Conclude the symmetry point as the vertex, $(x, f(x))$.

Now, let's work through each step:

Step 1: The quadratic function is $f(x) = -5x^2 + 10$. The coefficients are $a = -5$, $b = 0$, and $c = 10$.

Step 2: Applying the vertex formula $x = -\frac{b}{2a}$, we have:

$x = -\frac{0}{2(-5)} = 0$.

Step 3: Substitute $x = 0$ back into the function:

$f(0) = -5(0)^2 + 10 = 10$.

Step 4: Therefore, the vertex and symmetry point of the function is $(0, 10)$.

The correct choice from the given options is $(0,10)$.

Therefore, the solution to the problem is $(0,10)$.