To solve this problem, we follow these steps:
- Step 1: Identify the given dimensions of the trapezoid.
- Step 2: Use the formula for the area of a trapezoid.
- Step 3: Substitute the given values into the formula and calculate the area.
Now, let's work through these steps:
Step 1: We know from the problem that trapezoid ABCD has bases AB=5 and CD=8, with a height of AD=4.
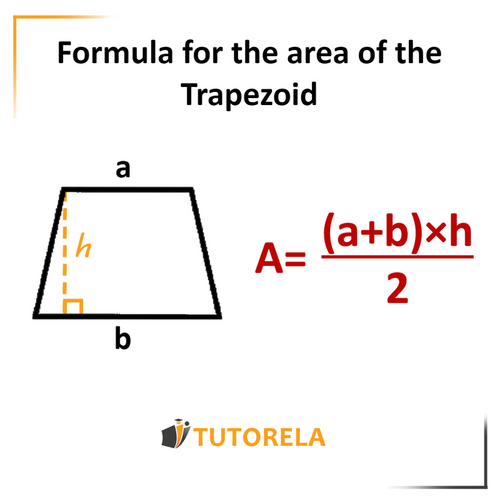
Step 2: The formula for the area of a trapezoid is:
A=21×(b1+b2)×h
Step 3: Plugging in the values:
A=21×(5+8)×4=21×13×4=252=26
Therefore, the area of the trapezoid ABCD is 26.