Perimeter of a Trapezoid Practice Problems with Solutions

Master trapezoid perimeter calculations with step-by-step practice problems. Learn formulas, solve missing side problems, and build confidence in geometry.

📚Master Trapezoid Perimeter Calculations
  • Calculate perimeter by adding all four sides of any trapezoid
  • Find missing side lengths when given the total perimeter
  • Apply Pythagorean theorem to complex trapezoid problems
  • Solve algebraic equations with variables in trapezoid sides
  • Work with isosceles trapezoids and their special properties
  • Connect trapezoid perimeter to real-world geometric applications

Understanding Perimeter of a Trapezoid

Complete explanation with examples

Perimeter of a trapezoid

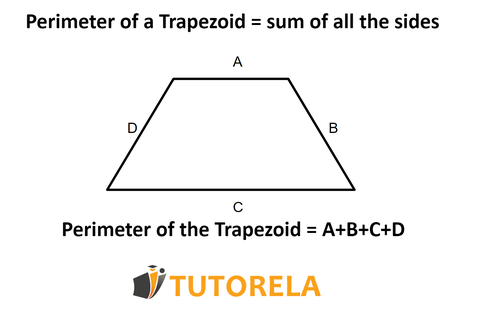
The trapezoid is a quadrilateral defined as having 2 parallel opposite sides. The calculation of the perimeter of the trapezoid is solved using a very simple formula that we will see below: all sides are added together. This type of questions can appear in tests of the first and second level in the first years of high school and also in final exams of level 3, 4 and 5 for the graduation of the secondary cycle.

A1- The_calculation_of_the_perimeter_of_the_trapezoid.

Detailed explanation

Practice Perimeter of a Trapezoid

Test your knowledge with 12 quizzes

The drawing shows an isosceles trapezoid.

What is its perimeter?

333555777

Examples with solutions for Perimeter of a Trapezoid

Step-by-step solutions included
Exercise #1

Look at the trapezoid in the diagram.

101010777121212777

What is its perimeter?

Step-by-Step Solution

In order to calculate the perimeter of the trapezoid we must add together the measurements of all of its sides:

7+10+7+12 =

36

And that's the solution!

Answer:

36

Video Solution
Exercise #2

Given the trapezoid:

444999666131313

What is its perimeter?

Step-by-Step Solution

The problem requires calculating the perimeter of the trapezoid by summing the lengths of its sides. Based on the given trapezoid diagram, the side lengths are clearly marked as follows:

  • First side: 4 4
  • Second side: 9 9
  • Third side: 6 6
  • Fourth side: 13 13

According to the formula for the perimeter of a trapezoid:

P=a+b+c+d P = a + b + c + d

Substituting the respective values:

P=4+9+6+13 P = 4 + 9 + 6 + 13

Calculating the sum, we find:

P=32 P = 32

Thus, the perimeter of the trapezoid is 32 32 .

Answer:

32

Video Solution
Exercise #3

What is the perimeter of the trapezoid in the figure?

444555999666

Step-by-Step Solution

To find the perimeter we will add all the sides:

4+5+9+6=9+9+6=18+6=24 4+5+9+6=9+9+6=18+6=24

Answer:

24

Video Solution
Exercise #4

What is the perimeter of the trapezoid in the figure?

7.57.57.54441.51.51.5333

Step-by-Step Solution

To find the perimeter of the trapezoid, we will sum the lengths of all its sides. The given side lengths are:

  • Base 1: 7.5 7.5
  • Base 2: 1.5 1.5
  • Leg 1: 3 3
  • Leg 2: 4 4

Using the formula for the perimeter P P of the trapezoid, we have:

P=a+b+c+d P = a + b + c + d

Substituting in the given values:

P=7.5+1.5+3+4 P = 7.5 + 1.5 + 3 + 4

Performing the addition:

P=7.5+1.5=9 P = 7.5 + 1.5 = 9

P=9+3=12 P = 9 + 3 = 12

P=12+4=16 P = 12 + 4 = 16

Therefore, the perimeter of the trapezoid is 16 16 .

Answer:

16

Video Solution
Exercise #5

Look at the trapezoid in the figure.

Calculate its perimeter.

2.52.52.510.410.410.45.35.35.3666

Step-by-Step Solution

To solve this problem, we'll follow these steps:

  • Step 1: Identify all given side lengths of the trapezoid.
  • Step 2: Apply the formula for the perimeter of the trapezoid.
  • Step 3: Sum up the lengths to find the perimeter.

Now, let's work through each step:
Step 1: The problem gives us the lengths of the trapezoid's sides:
- AB=2.5 AB = 2.5
- BC=10.4 BC = 10.4
- CD=5.3 CD = 5.3
- DA=6 DA = 6

Step 2: We use the formula for the perimeter of a trapezoid:

P=AB+BC+CD+DA P = AB + BC + CD + DA

Step 3: Plugging in the given values, we calculate:

P=2.5+10.4+5.3+6 P = 2.5 + 10.4 + 5.3 + 6

Calculating further, we have:

P=24.2 P = 24.2

Therefore, the perimeter of the trapezoid is 24.2 24.2 .

Answer:

24.2

Video Solution

Frequently Asked Questions

Everything you need to know about Perimeter of a Trapezoid

What is the formula for finding the perimeter of a trapezoid?

+
The perimeter of a trapezoid is found by adding all four sides: P = a + b + c + d, where a, b, c, and d represent the lengths of each side. This simple addition formula works for any trapezoid, regardless of whether it's isosceles, scalene, or right-angled.

How do you find a missing side when you know the trapezoid's perimeter?

+
To find a missing side, subtract the sum of the known sides from the total perimeter. For example, if the perimeter is 30 and three sides are 7, 5, and 10, then the missing side = 30 - (7 + 5 + 10) = 8 units.

What's the difference between trapezoid perimeter and area formulas?

+
Perimeter measures the distance around the trapezoid by adding all sides (P = a + b + c + d). Area measures the space inside using the formula A = (b₁ + b₂) × h ÷ 2, where b₁ and b₂ are the parallel bases and h is the height.

Do I need to know which sides are parallel to find the perimeter?

+
No, you don't need to identify the parallel sides (bases) to calculate perimeter. Simply add all four side lengths together. The parallel sides are only important when calculating area or working with specific trapezoid properties.

How do you solve trapezoid perimeter problems with variables?

+
Set up an equation where the sum of all sides equals the given perimeter. For example, if sides are 6, x, x+1, and 10 with perimeter 26, write: 6 + x + (x+1) + 10 = 26. Solve by combining like terms: 2x + 17 = 26, so x = 4.5.

When do you use the Pythagorean theorem in trapezoid perimeter problems?

+
Use the Pythagorean theorem when you need to find the length of a non-parallel side (leg) and you know the height and horizontal distance. This often occurs in right trapezoids or when trapezoids are parts of rectangles or triangles.

What are common mistakes students make with trapezoid perimeter?

+
Common mistakes include: 1) Confusing perimeter and area formulas, 2) Only adding the parallel sides instead of all four sides, 3) Forgetting to include units in the final answer, 4) Not properly setting up equations when solving for missing sides.

How is trapezoid perimeter used in real-world applications?

+
Trapezoid perimeter calculations are used in construction for calculating fencing around trapezoidal plots, determining trim lengths for trapezoidal windows, measuring borders for landscaping projects, and calculating material needs for trapezoidal roof sections or building foundations.

More Perimeter of a Trapezoid Questions

Click on any question to see the complete solution with step-by-step explanations

Perimeter of a Trapezoid

Calculate Trapezoid Perimeter: Inside an Isosceles Triangle with Height 8 Compare Two Trapezoids: Analyzing Measurements x+5, 17, and Variable y Compare Trapezoids: Are Two Trapezoids with Sides x and x+16 Congruent? Calculate the Missing Side in a Trapezoid with 25cm Perimeter Isosceles Trapezoid: Finding Perimeter Given Area=9cm² and Parallel Sides 3,6

Continue Your Math Journey

Master Perimeter of a Trapezoid first, then advance to these related topics that build on your fraction skills

Suggested Topics to Practice in Advance

AreaTrapezoidsArea of a trapezoidAreas of Polygons for 7th GradeArea of a right-angled trapezoidArea of an isosceles trapezoidHow do we calculate the area of complex shapes?

Topics Learned in Later Sections

PerimeterHow do we calculate the perimeter of polygons?

Practice by Question Type

Choose your preferred learning style and practice format for fraction problems
Applying the formula Calculate The Missing Side based on the formula Comparison between 2 of the same shape with an identical perimeter Finding Area based off Perimeter and Vice Versa Using variables