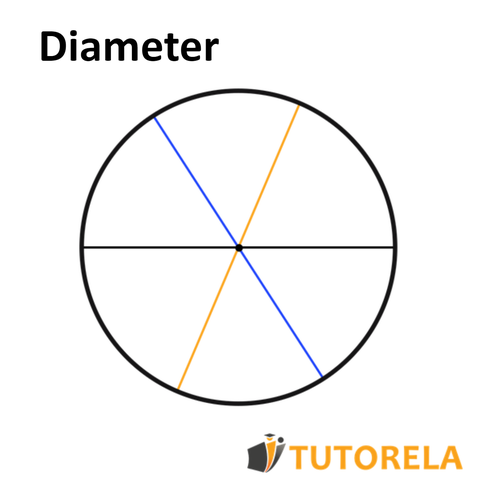
A diameter is a section that connects two points that lie on the circumference, that passes through the center of the circle. The diameter is actually twice the radius.
As in the case of the radius, as well as in the case of the diameter, there are an infinite number of diameters on the circumference, and all are identical in length.
Below is an example of a circle with several diameters marked in different colors.
There are only 4 radii in a circle.
Is there sufficient data to determine that
\( GH=AB \)
M is the center of the circle.
Perhaps \( AB=CD \)
In which of the circles is the center of the circle marked?
M is the center of the circle.
Perhaps \( MF=MC \)
There are only 4 radii in a circle.
A radius is a straight line that connects the center of the circle with a point on the circle itself.
Therefore, the answer is incorrect, as there are infinite radii.
False
Is there sufficient data to determine that
No
M is the center of the circle.
Perhaps
No
In which of the circles is the center of the circle marked?
M is the center of the circle.
Perhaps
Yes
M is the center of the circle.
In the figure we observe 3 diameters?
M is the center of the circle below.
\( AB=10 \)
Can a chord with a length of 15 cm be drawn in the circle?
M is the center of the circle shown below.
AB is a chord in the circle and is 8 long.
Which of the options is a reasonable length for circle's diameter?
Is it possible that the circumference of a circle is 8 meters and its diameter is 4 meters?
M is the center of the circle.
Perhaps \( CM+MD=2EM \)
M is the center of the circle.
In the figure we observe 3 diameters?
No
M is the center of the circle below.
Can a chord with a length of 15 cm be drawn in the circle?
No
M is the center of the circle shown below.
AB is a chord in the circle and is 8 long.
Which of the options is a reasonable length for circle's diameter?
Is it possible that the circumference of a circle is 8 meters and its diameter is 4 meters?
Impossible
M is the center of the circle.
Perhaps
Yes
Perhaps \( MF+MD=AB \)
M is the center of the circle.
Is AB the diameter?
M is the center of the circle.
Perhaps \( 0.5DC=EM \)
Perhaps \( P=\pi\times EF \)
Is it possible that a circle with a circumference of 50.6 meters has a diameter of 29 meters?
Perhaps
No
M is the center of the circle.
Is AB the diameter?
No
M is the center of the circle.
Perhaps
Yes
Perhaps
Yes
Is it possible that a circle with a circumference of 50.6 meters has a diameter of 29 meters?
No.