Radius - Examples, Exercises and Solutions

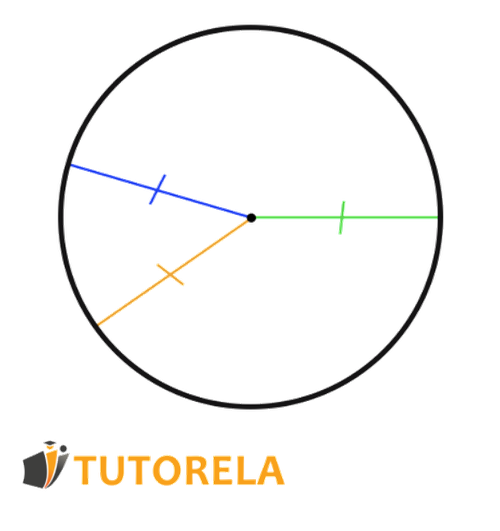
The radius is one of the many elements that exist in a circle. The radius is a segment that connects the center of the circle with any point located on the circle itself. Each circle has an infinite number of radii and their length is exactly the same, that is, they are identical.

The radius is used to calculate the diameter and perimeter of the circle, it is also used to obtain the area of the circle.

Below are several examples of different circumferences.

The colored parts are, in fact, some radii painted on each circumference:

The colored parts are, in fact, some painted radii on the circumference:

Practice Radius

Question 1

There are only 4 radii in a circle.

Question 2

Which figure shows the radius of a circle?

Question 3

Which diagram shows a circle with a point marked in the circle and not on the circle?

Question 4

M is the center of the circle.

Perhaps $$ AB=CD $$

Question 5

Is it possible that the circumference of a circle is 8 meters and its diameter is 4 meters?

Examples with solutions for Radius

Exercise #1

There are only 4 radii in a circle.

Step-by-Step Solution

A radius is a straight line that connects the center of the circle with a point on the circle itself.

Therefore, the answer is incorrect, as there are infinite radii.

Answer

False

Exercise #2

Which figure shows the radius of a circle?

Step-by-Step Solution

It is a straight line connecting the center of the circle to a point located on the circle itself.

Therefore, the diagram that fits the definition is c.

In diagram a, the line does not pass through the center, and in diagram b, it is a diameter.

Answer

Exercise #3

Which diagram shows a circle with a point marked in the circle and not on the circle?

Step-by-Step Solution

The interpretation of "in a circle" is inside the circle.

In diagrams a'-d' the point is on the circle, and in diagram c' the point is outside the circle.

Answer

Exercise #4

M is the center of the circle.

Perhaps $AB=CD$

Video Solution

Step-by-Step Solution

CD is a diameter, since it passes through the center of the circle, meaning it is the longest segment in the circle.

AB does not pass through the center of the circle and is not a diameter, therefore it is necessarily shorter.

Therefore:

$AB\ne CD$

Answer

Exercise #5

Is it possible that the circumference of a circle is 8 meters and its diameter is 4 meters?

Video Solution

Step-by-Step Solution

To calculate, we will use the formula:

$\frac{P}{2r}=\pi$

Pi is the ratio between the circumference of the circle and the diameter of the circle.

The diameter is equal to 2 radii.

Let's substitute the given data into the formula:

$\frac{8}{4}=\pi$

$2\ne\pi$

Therefore, this situation is not possible.

Answer

Impossible

Question 1

Is there sufficient data to determine that

$$ GH=AB $$

Question 2

In which of the circles is the center of the circle marked?

Question 3

M is the center of the circle.

Perhaps $$ MF=MC $$

Question 4

M is the center of the circle.

In the figure we observe 3 diameters?

Question 5

M is the center of the circle below.

$$ AB=10 $$

Can a chord with a length of 15 cm be drawn in the circle?

Exercise #6

Is there sufficient data to determine that

$GH=AB$

Video Solution

Answer

Exercise #7

In which of the circles is the center of the circle marked?

Video Solution

Answer

Exercise #8

M is the center of the circle.

Perhaps $MF=MC$

Video Solution

Answer

Yes

Exercise #9

M is the center of the circle.

In the figure we observe 3 diameters?

Video Solution

Answer

Exercise #10

M is the center of the circle below.

$AB=10$

Can a chord with a length of 15 cm be drawn in the circle?

Video Solution

Answer

Question 1

M is the center of the circle shown below.

AB is a chord in the circle and is 8 long.

Which of the options is a reasonable length for circle's diameter?

Question 2

M is the center of the circle.

Perhaps $$ CM+MD=2EM $$

Question 3

Perhaps $$ MF+MD=AB $$

Question 4

M is the center of the circle.

Is AB the diameter?

Question 5

M is the center of the circle.

Perhaps $$ 0.5DC=EM $$

Exercise #11

M is the center of the circle shown below.

AB is a chord in the circle and is 8 long.

Which of the options is a reasonable length for circle's diameter?

Video Solution

Answer

$16$

Exercise #12

M is the center of the circle.

Perhaps $CM+MD=2EM$

Video Solution

Answer

Yes

Exercise #13

Perhaps $MF+MD=AB$

Video Solution

Answer

Exercise #14

M is the center of the circle.

Is AB the diameter?

Video Solution

Answer

Exercise #15

M is the center of the circle.

Perhaps $0.5DC=EM$

Video Solution

Answer

Yes

Topics learned in later sections