The radius is the distance from the center point of the circle to any point on its circumference, it is denoted by and it equals half the diameter.
Parts of a Circle Practice Problems with Solutions
Master circle geometry with practice problems on radius, diameter, circumference, and area. Step-by-step solutions included for complete understanding.
📚Master Circle Parts Through Interactive Practice
- Calculate radius and diameter using the relationship between these measurements
- Apply circumference formulas using both radius and diameter methods
- Solve area problems using the pi × r² formula with step-by-step guidance
- Identify perpendicular properties and their effects on chords and arcs
- Work with pi (3.14) in real-world circle measurement problems
- Practice converting between different circle measurements and units
Understanding Parts of the Circle
Complete explanation with examples
Parts of a Circle
Circle radius
The diameter of the circle
The diameter is a straight line that passes through the center point of the circle and connects points on the circumference. The diameter equals twice the radius.
Pi
Pi is a constant number that represents the ratio between a circle's circumference and its diameter.
Its symbol is and it is always equal to .
perpendicular
A perpendicular is a straight line that extends from the center of the circle to any chord in the circle, divides the chord into equal parts, creates right angles with the chord, and bisects the arc corresponding to the chord.
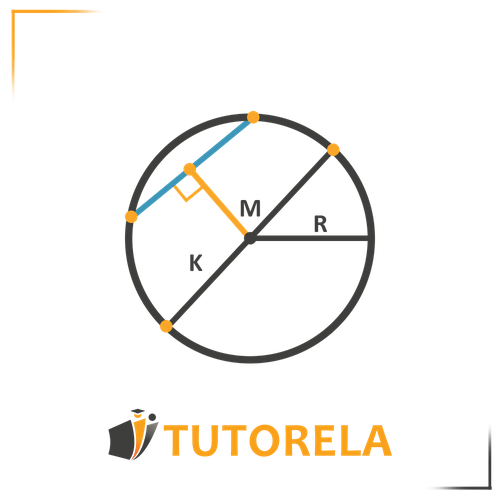
- center of the circle
- radius of the circle
- diameter of the circle
Blue line - chord
Orange line - perpendicular
Practice Parts of the Circle
Test your knowledge with 11 quizzes
True or false:
The radius of a circle is the chord.
Examples with solutions for Parts of the Circle
Step-by-step solutions included
Exercise #1
M is the center of the circle.
Perhaps
Step-by-Step Solution
CD is a diameter, since it passes through the center of the circle, meaning it is the longest segment in the circle.
AB does not pass through the center of the circle and is not a diameter, therefore it is necessarily shorter.
Therefore:
Answer:
No
Video Solution
Exercise #2
Which figure shows the radius of a circle?
Step-by-Step Solution
It is a straight line connecting the center of the circle to a point located on the circle itself.
Therefore, the diagram that fits the definition is c.
In diagram a, the line does not pass through the center, and in diagram b, it is a diameter.
Answer:
Exercise #3
Which diagram shows a circle with a point marked in the circle and not on the circle?
Step-by-Step Solution
The interpretation of "in a circle" is inside the circle.
In diagrams (a) and (d) the point is on the circle, while in diagram (c) the point is outside of the circle.
Answer:
Exercise #4
The number Pi represents the relationship between which parts of the circle?
Step-by-Step Solution
To solve this problem, we will clarify the relationship between the constant and parts of a circle.
The number is a constant that relates the circumference of a circle (the perimeter) to its diameter. The formula for the circumference of a circle is given by:
where is the circumference, and is the diameter of the circle. This equation shows that is the ratio of the circumference of a circle to its diameter, which remains constant for all circles.
Therefore, indeed represents the relationship between the circle’s perimeter and its diameter.
Thus, the correct answer is: Perimeter and diameter
Answer:
Perimeter and diameter
Exercise #5
All ____ about the circle located in the distance ____ from the ____ circle
Step-by-Step Solution
To solve this problem, we will consider the parts of a circle and how they interplay based on the description provided in the incomplete sentence:
- Step 1: Recognize that the first blank needs a term that refers to the primary element defining a circle externally.
- Step 2: The second blank needs a term associated with 'equal' as it describes distances from a specific location, hinting at a property of circles.
- Step 3: The third blank likely wants us to relate this location to the circle itself, denoting the standard geometric reference point.
Now, let's fill in each blank systematically:
The first term 'Point' refers to all points lying on the perimeter of a circle. In the definition of a circle, each point on the circle’s circumference maintains an equal distance from its center.
The second term 'equal' pertains to how all these points are at an equal distance - which is the radius - from the center.
The third term 'center' specifies the reference point within the circle from which every point on the circle is equidistant.
Thus, the complete statement is: "All point about the circle located in the distance equal from the center circle."
The correct choice that completes the sentence is: Point, equal, center.
Answer:
Point, equal, center
Frequently Asked Questions
What is the difference between radius and diameter of a circle?
+The radius extends from the center to any point on the circumference, while the diameter is a straight line passing through the center connecting two points on the circumference. The diameter is always twice the radius (d = 2r).
How do you calculate the circumference of a circle?
+Use the formula: Circumference = 2 × π × radius OR Circumference = π × diameter. Since π = 3.14, if the radius is 5 cm, the circumference would be 2 × 3.14 × 5 = 31.4 cm.
What does a perpendicular from the center to a chord do?
+A perpendicular from the center to a chord: 1) Divides the chord into two equal parts, 2) Creates two right angles (90°) with the chord, 3) Bisects the corresponding arc on the circumference.
How do you find the area of a circle step by step?
+Follow these steps: 1) Identify the radius, 2) Square the radius (multiply by itself), 3) Multiply by π (3.14). Formula: Area = π × r². Example: if r = 4, then Area = 3.14 × 4² = 3.14 × 16 = 50.24 square units.
Why is pi always 3.14 in circle calculations?
+Pi (π) represents the constant ratio between any circle's circumference and its diameter. While the exact value has infinite decimal places, we use 3.14 as an approximation for most calculations to keep problems manageable.
If I know the diameter, how do I find the radius quickly?
+Simply divide the diameter by 2. Since diameter = 2 × radius, then radius = diameter ÷ 2. For example, if the diameter is 18 cm, the radius is 18 ÷ 2 = 9 cm.
What are the most common mistakes when solving circle problems?
+Common errors include: 1) Confusing radius and diameter measurements, 2) Forgetting to square the radius in area calculations, 3) Using the wrong circumference formula, 4) Not including units in final answers.
How can I remember circle formulas for tests?
+Use these memory tricks: Circumference has 'C' like 'Circle around' (2πr), Area has 'A' like 'All inside' (πr²). Remember that circumference measures the edge while area measures the space inside the circle.