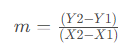Finding a linear equation is actually about graphing the linear function using or .

We can find the linear equation in ways:
- Using a point on the line and the slope of the line.
- Using two points that lie on the line.
- Using the graph of the function itself.
- Using parallel lines, that is, if the requested line is parallel to another line and we know the slope of the other line.
- Using perpendicular lines, that is, if the requested line is perpendicular to another line and we know the slope of the other line.
The first three methods are based in one way or another on the general formula for finding the linear equation:
The last two methods also use this formula, but they also take into account two additional rules:
- For parallel lines, the slopes are equal, that is
- For perpendicular lines, the slopes have the relationship