The collateral angles are a pair of angles that we can find on the same side of a transversal or secant line that intersects two parallel lines, and that are also internal or external with respect to the parallel lines. The sum of the collateral angles equals.
Collateral angles
Test yourself on angles in parallel lines!
Identify the angle shown in the figure below?
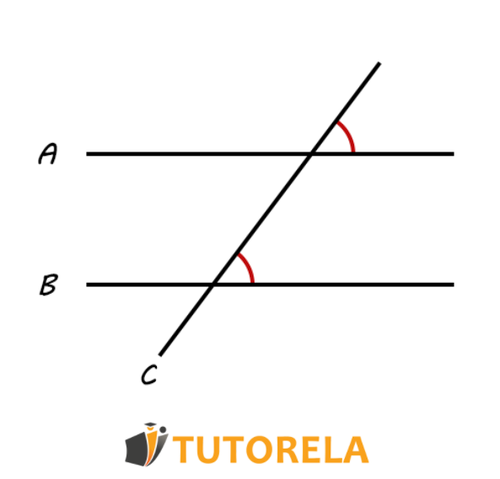
Before we touch on the subject of collateral angles, let's see the circumstances that could lead us to use them. Let's imagine two parallel lines and a transversal line (for a more detailed explanation you should take a look at the article "Parallel lines" where this subject is discussed in depth), as we can see in the following illustration:
In the illustration you can see the two parallel lines and together with the transversal that intersects them. In these circumstances it is very common to find collateral angles.
Now we will define the collateral angles in a more precise way that will help us to recognize them with greater certainty:
The collateral angles are the pair of angles that we can find on the same side of a transversal line that intersects two parallel lines and that are either internal or external with respect to the parallel lines. The sum of the collateral angles equals .
In the following illustration we can see two pairs of collateral angles. We have marked the first pair in blue and the second pair in red:
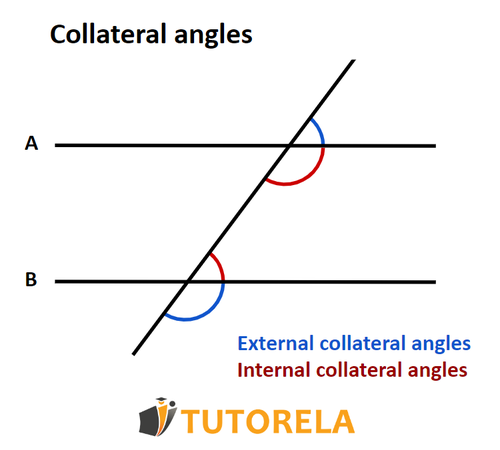
Note that if the pair of collateral angles are outside the parallel lines then they are called external collateral angles, and if they are inside the parallel lines they are called internal collateral angles.
We still have more types of angles in the pipeline
The illustration above leads us to other types of angles. In the following, we will briefly describe a few:
Identify the angles shown in the diagram below?
Which type of angles are shown in the figure below?
Which type of angles are shown in the diagram?
Alternate angles
Alternate angles are a pair of angles that can be found on opposite sides of a transversal that intersects two parallel lines. These angles are also on opposite sides of the parallel line to which they belong, and they are equal. If you need more detailed information, you can have a look at the article specially dedicated to this subject "Alternate angles".
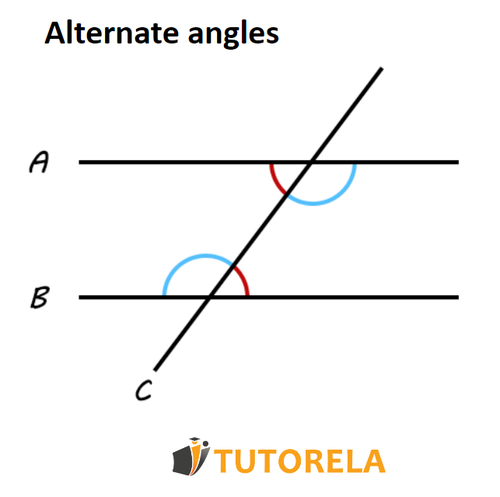
Corresponding angles
The corresponding angles are a pair of angles that we can find on the same side of a transversal that intersects two parallel lines. These angles are on the same side of the parallel line to which they belong and are equal.
If you need more detailed information you can have a look at the article specially dedicated to this subject "Corresponding angles".
Which pair of angles is described in the drawing?
What type of angles are shown below given that lines a and b are parallel?
What type of angles are shown below given that a and b are parallel lines?
Opposite angles
Opposite angles arise at the point of intersection of two intersecting straight lines, facing each other, sharing the same vertex. Opposite angles are equal. If you need more detailed information you can have a look at the article specially dedicated to this subject " Vertically opposite angles".

If you are interested in learning more about other types of angles, you can access one of the following articles:
- Angle notation
- Sides, vertices, and angles
- Bisector
- Right angle
- Acute angle
- Obtuse angle
- Plane angle
- Adjacent angles
- Vertically opposite angles
- Alternate angles
- Corresponding angles
- Sum of the angles of a triangle
- Sum of the angles of a polygon
- Addition and difference of angles
On Tutorela website, you will find a variety of articles about mathematics.
Examples with collateral angles
Exercise 1
You have to determine, in each of the illustrations below, if they are collateral angles or not.
Please explain your answer.
Solution:
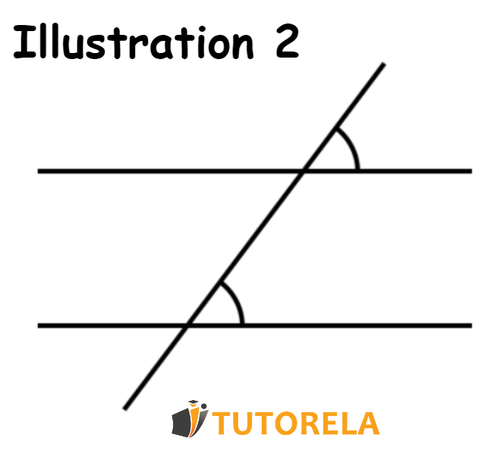
Illustration No 1
In this illustration we indeed have a pair of collateral angles, since the two criteria that describe them are met. First, there is a pair of angles located on the same side of the transversal that intersects two parallel lines. Secondly, these angles are at opposite sides of the parallel line to which they belong.
Illustration No 2
In this illustration we are not dealing with collateral angles since one of the two criteria that describes them is not met, that is to say, we do have a pair of angles located on the same side of the transversal that intersects the two parallel lines. But, these angles are on the same side of the parallel line to which they belong.
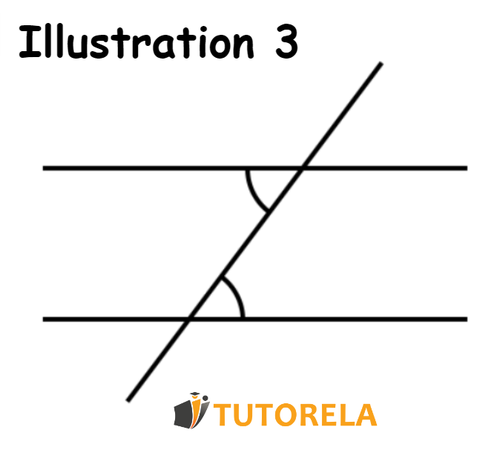
Illustration No 3
In this illustration we are not dealing with collateral angles since one of the two criteria that describe them is not met, that is to say, there is a pair of angles that are at opposite sides of the parallel line to which they belong. However, these angles are located on different sides of the transversal that intersects the two parallel lines.
So:
Illustration No 1: collateral angles.
Illustration No 2: they are not collateral angles, however, they are corresponding angles.
Illustration No 3: they are not collateral angles, however, they are alternate angles.
Which angles are marked in the figure?
\( a \) is parallel to
\( b \)
Determine which of the statements is correct.
Lines a and b are parallel.
Which of the following angles are co-interior?
Exercise 2
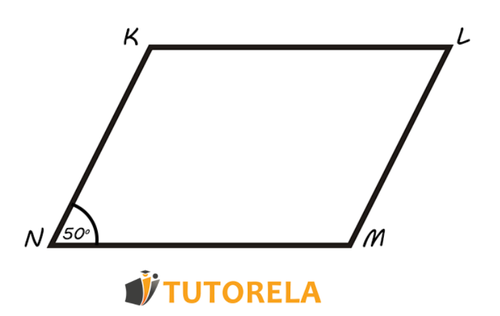
Given the parallelogram as shown in this illustration.
The angle of the parallelogram measures .
Calculate the other angles of the parallelogram .
Solution:
Since we are shown a parallelogram, we can take advantage of its properties to calculate the rest of the angles based on the angle .
In a parallelogram the opposite angles are equal, therefore, from this we can deduce that also the angle measures .
Now let's move on to the other two angles. The opposite sides of a parallelogram are parallel, i.e., side is parallel to the side . It follows that the angles and are, in fact, a pair of collateral angles, i.e., they are a pair of angles located on the same side of the transversal () that intersects two parallel lines ( and ). Secondly, these angles are at opposite sides of the parallel line to which they belong. The collateral angles are supplementary, i.e., together they equal . Therefore we have that the angle measures .
The angles and are also opposites within a parallelogram, so they are equal, i.e. the angle also measures .
Then:
The angle measures .
The angle measures .
The angle measures .
Exercise 3
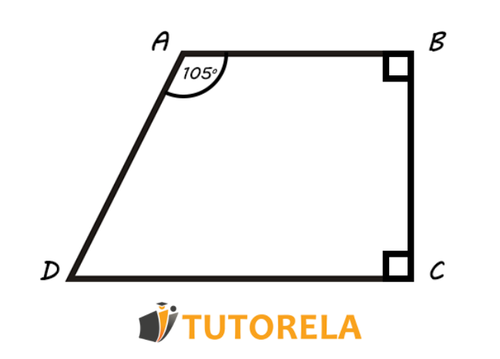
Given the right trapezoid as described in the illustration.
The angle of the trapezoid measures .
What is angle ?
Solution:
We have a right trapezoid. This data is very important to solve our exercise.
Why is it important? Since it is a trapezoid, we have two parallel bases, that is, and .
Having two parallel bases implies that the angles and are, in fact, collateral angles, i.e., we have a pair of angles located on the same side of the transversal (the side ) that intersects two parallel lines ( and ). Moreover, these angles are at the opposite level with respect to the parallel line to which they belong. As we have learned, the collateral angles are supplementary, that is, together they equal . Therefore, we have that the angle measures .
Then:
The angle measures .
Look at the angles shown in the figure below.
What is their relationship?
\( \)
The lines in the figure are parallel.
Are the angles \( \alpha \) and \( \beta \) corresponding?
The lines in the figure are parallel.
Are the angles \( \alpha \) and \( \beta \) corresponding?
Exercise 4
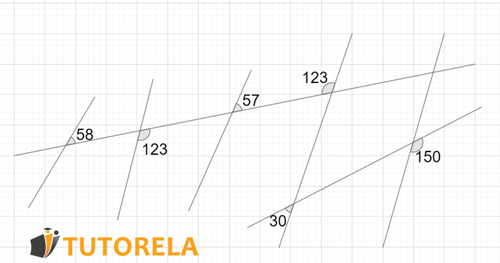
How many parallel lines are there in the figure?
Solution:
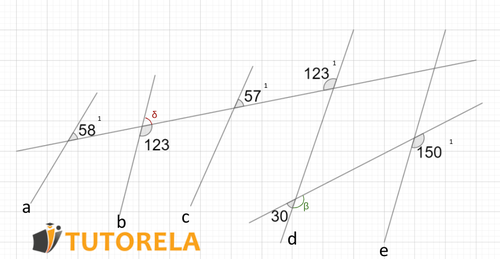
Let's start by seeing if the straight lines "" and "" are parallel:
Assuming that both lines are parallel, we have a transversal that intersects them, forming an angle of at the intersection with the line "" and an angle of at the intersection with the line "". Then, the opposite angle to the angle of together with the angle of should form a pair of collateral angles, i.e., together they should add up to . Remembering that opposite angles are equal, we see that the sum does not add up to because . Therefore, the lines "" and "" are not parallel.
Now let's see if the lines "" and "" are parallel:
Using similar reasoning as above, we can assume that these lines are parallel. Then using the opposite angle to the angle of formed by the straight line "", and the angle of formed by the straight line "", we see that they are internal collaterals, so their sum should be . In this case this is true since therefore the lines "" and "" are parallel.
Now let's see if the lines "" and "" are parallel:
The angle of formed by the line "" and the angle of formed by the line "" are internal collateral angles, so their sum should be . In this case this is true since therefore the lines "" and "" are parallel.
Now let's see if the lines "" and "" are parallel:
Again, let's assume that they are. The angle of formed by the line "" and the angle of formed by the line "" form external collateral angles, therefore, toether they should equal . This is true because Therefore, the lines "" and "" are parallel.
Then:
The straight lines " " are parallel.
Exercise 5
Given the parallel lines , .
Calculate the marked angles.
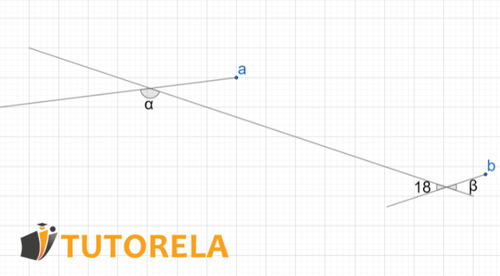
Solution:
Angle is opposite to the angle that equals .
The angle of happens to be internal collateral with angle α, so their sum must equal :
Then:
The angles are y .
The lines in the figure are parallel.
Are the angles \( \alpha \) and \( \beta \) corresponding?
The lines in the figure are parallel.
Are the angles \( \alpha \) and \( \beta \) corresponding?
Identify the angle shown in the figure below?
Exercise 6
Given the trapezoid, find the value of .
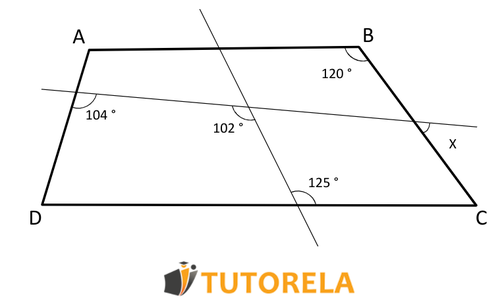
Solution:
Since the sides y are parallel, the angles formed by the transversal lines will be:
The angles \( \sphericalangle2 \) and \( \sphericalangle6 \) are opposite angles, so they are equal:
In the same way, the angles and are opposite angles, so they are equal.
Then, remembering that the sum of the angles of a quadrilateral is equal to we have that:
Therefore:
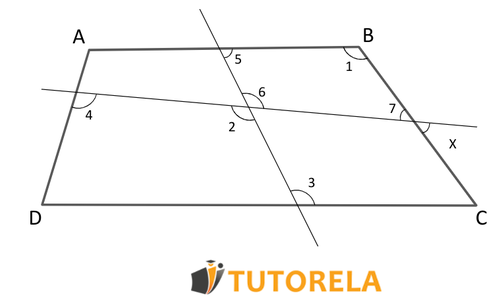
Then:
Exercise 7
Given the polygon in the figure:
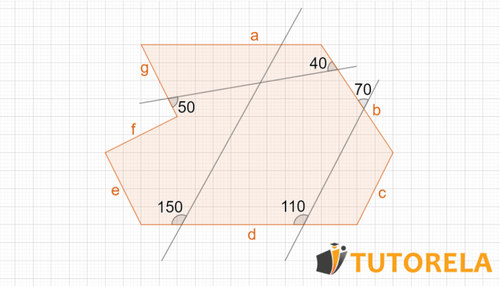
Which of the straight lines are parallel to each other?
Solution:
- Between the sides "" and "" we can identify a pair of internal alternate angles that are not equal, therefore those sides are not parallel.
- Considering the angles formed by the transversal that intersects the sides "" and "", we have that the opposite angle to the angle of is internal alternate to the angle of That means they should be equal if "" and "" were parallel, which we can see does not occur.
- There is no data on "" and "" because there is no transversal line that intersects them, the same goes for the other pairs of sides.
Exercise 8:
is parallel to
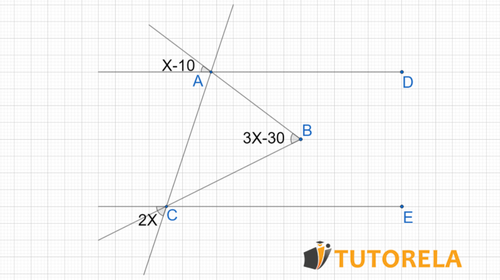
What is the value of if it is given that is an isosceles triangle, with sides
Solution:
The angle is opposite to the angle therefore they are equal.
By the same argument the angle is equal to .
Then, the sum of the internal alternate angle to the angle together with the angle and the angle add up to
We have the following equation:
Now, since the sides then the angles .
Next, recall that the sum of the interior angles of a triangle is therefore:
Identify the angles shown in the diagram below?
Which type of angles are shown in the figure below?
Which type of angles are shown in the diagram?
Questions on the subject
What are collateral angles?
They are a pair of angles that we can find on the same side of a transversal or secant line that intersects two parallel lines and that are either internal or external with respect to the parallel lines.
Where do the collateral angles appear?
When two parallel lines are intersected by a transversal or secant line.
What is the sum of a pair of collateral angles?
Being supplementary angles, their sum is .
Which pair of angles is described in the drawing?
What type of angles are shown below given that lines a and b are parallel?
What type of angles are shown below given that a and b are parallel lines?
Examples with solutions for Collateral angles
Exercise #1
Identify the angle shown in the figure below?
Step-by-Step Solution
Remember that adjacent angles are angles that are formed when two lines intersect one another.
These angles are created at the point of intersection, one adjacent to the other, and that's where their name comes from.
Adjacent angles always complement one another to one hundred and eighty degrees, meaning their sum is 180 degrees.
Answer
Adjacent
Exercise #2
Identify the angles shown in the diagram below?
Step-by-Step Solution
Let's remember that vertical angles are angles that are formed when two lines intersect. They are are created at the point of intersection and are opposite each other.
Answer
Vertical
Exercise #3
Which type of angles are shown in the figure below?
Step-by-Step Solution
Alternate angles are a pair of angles that can be found on the opposite side of a line that cuts two parallel lines.
Furthermore, these angles are located on the opposite level of the corresponding line that they belong to.
Answer
Alternate
Exercise #4
Which type of angles are shown in the diagram?
Step-by-Step Solution
First let's remember that corresponding angles can be defined as a pair of angles that can be found on the same side of a transversal line that intersects two parallel lines.
Additionally, these angles are positioned at the same level relative to the parallel line to which they belong.
Answer
Corresponding
Exercise #5
is parallel to
Determine which of the statements is correct.
Video Solution
Step-by-Step Solution
Let's review the definition of adjacent angles:
Adjacent angles are angles formed where there are two straight lines that intersect. These angles are formed at the point where the intersection occurs, one next to the other, and hence their name.
Now let's review the definition of collateral angles:
Two angles formed when two or more parallel lines are intersected by a third line. The collateral angles are on the same side of the intersecting line and even are at different heights in relation to the parallel line to which they are adjacent.
Therefore, answer C is correct for this definition.
Answer
Colaterales Adjacent
More Questions
Angles in Parallel Lines
- Adjacent Angle Identification: Analyzing Line Intersection Diagram
- Adjacent Angles: Identifying Intersecting Lines in Geometric Diagram
- Adjacent Angles: Analyzing Intersecting Lines in Geometric Diagram
- Adjacent Angle Identification: Analyzing Geometric Line Intersections
- Adjacent Angles: Analyzing Line Segment Diagram for Angle Properties
- Area
- Trapezoids
- Area of a trapezoid
- Perimeter of a trapezoid
- Parallelogram
- The area of a parallelogram: what is it and how is it calculated?
- Perimeter of a Parallelogram
- Kite
- Area of a Deltoid (Kite)
- Parallel lines
- Rectangle
- Calculating the Area of a Rectangle
- The perimeter of the rectangle
- Congruent Rectangles
- The sides or edges of a triangle
- Triangle Height
- Sides, Vertices, and Angles
- Angle Notation
- Angle Bisector
- Types of Angles
- Right angle
- Acute Angles
- Obtuse Angle
- Plane angle
- Sum and Difference of Angles
- Sum of Angles in a Polygon
- The Sum of the Interior Angles of a Triangle
- Perpendicular Lines
- Exterior angles of a triangle
- Perimeter
- Triangle
- Types of Triangles
- Obtuse Triangle
- Equilateral triangle
- Identification of an Isosceles Triangle
- Scalene triangle
- Acute triangle
- Isosceles triangle
- The Area of a Triangle
- Area of a right triangle
- Area of Isosceles Triangles
- Area of a Scalene Triangle
- Area of Equilateral Triangles
- Perimeter of a triangle
- Areas of Polygons for 7th Grade
- Right Triangle
- Area of a right-angled trapezoid
- Area of an isosceles trapezoid
- Median in a triangle
- Center of a Triangle - The Centroid - The Intersection Point of Medians
- How do we calculate the area of complex shapes?
- How to calculate the area of a triangle using trigonometry?
- How do we calculate the perimeter of polygons?
- All terms in triangle calculation
- Types of angles (right, acute, obtuse, straight)









