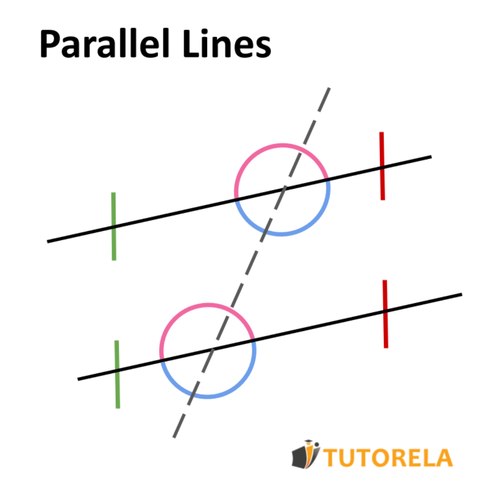
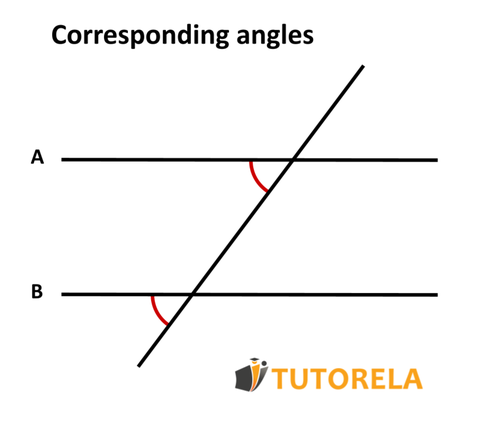
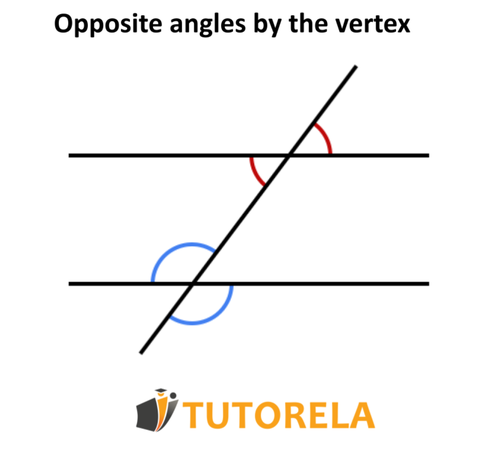
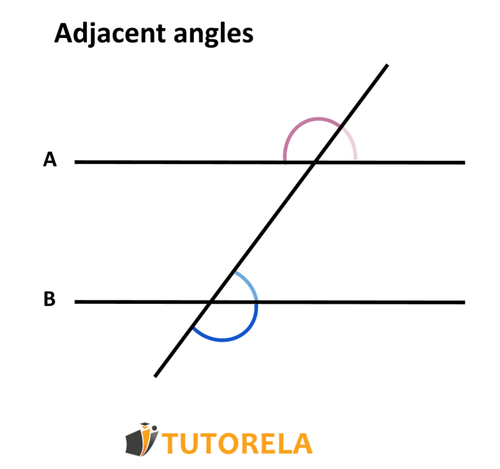
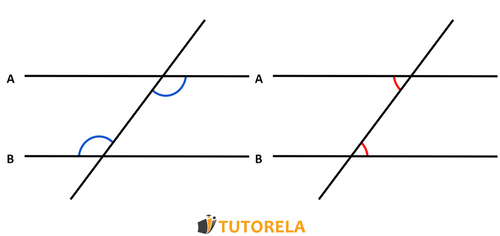
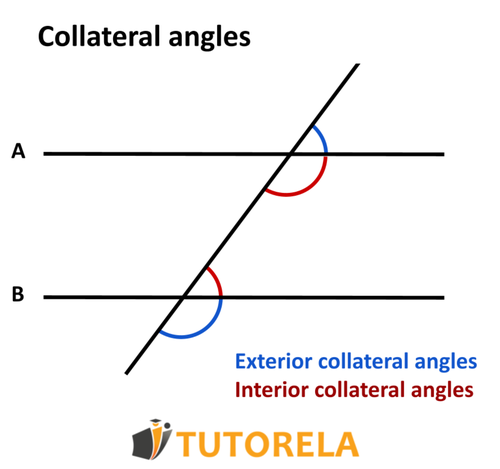
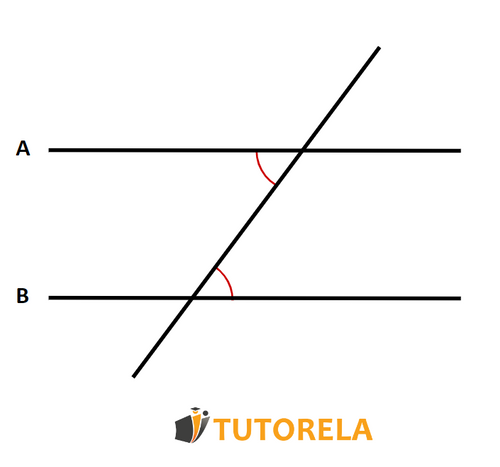
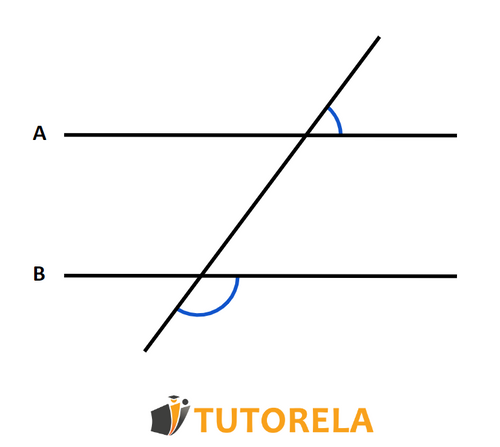
The sum of adjacent angles is 180 degrees.
To solve this problem, let's first understand the concept of adjacent angles. Adjacent angles share a common vertex and a common side. When two adjacent angles are formed by two intersecting lines, they often form what is known as a linear pair.
According to the Linear Pair Postulate, if two angles form a linear pair, then the sum of these adjacent angles is 180 degrees. This is because these angles lie on a straight line, effectively forming a straight angle, which measures 180 degrees.
Let's apply this knowledge to the statement in the problem:
The statement says, "The sum of adjacent angles is 180 degrees." In the context of the Linear Pair Postulate, this is indeed correct as adjacent angles that create a linear pair sum to 180 degrees.
Therefore, when the statement refers specifically to linear pairs, it is true.
Thus, the solution to the problem is True.