Alternate interior angles

In this article, we will learn about alternate interior angles, how to identify them, as well as their characteristics.
First, we need to remember what alternate angles are in general:
Alternate angles
Alternate angles between parallel lines are equal.
They are called alternate angles because they:
• Are not on the same side of the transversal line
• Are not on the same "level" relative to the line

Here are alternate angles for example:

The two marked angles are not on the same level and not on the same side, therefore they are alternate angles.
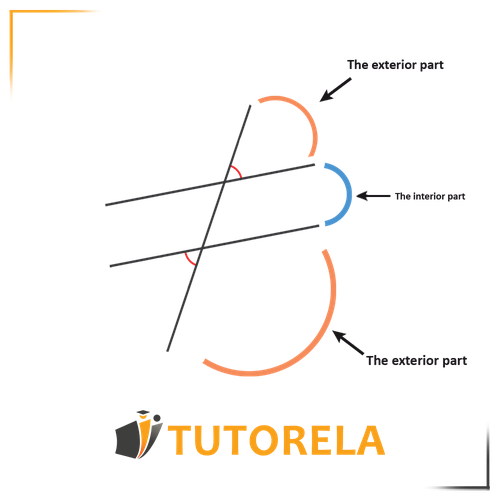
In order to confirm the presence of an alternate interior angle, you must observe that:
There is an exterior part - outside the two parallel lines
As well as an interior part - between the two parallel lines.
Let's examine the illustration:

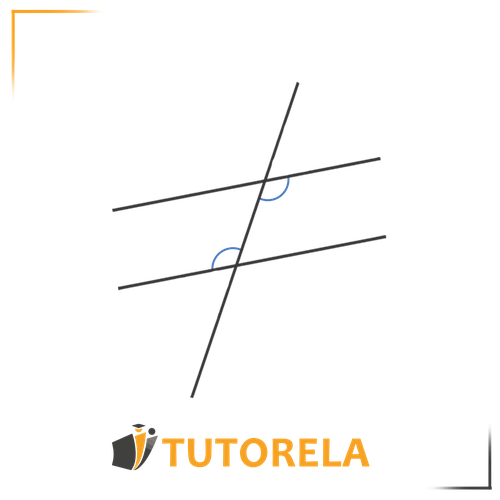
In the illustration, we can see that the two alternate angles located between the two parallel lines in the inner part are alternate interior angles. Let's examine another example of a pair of alternate interior angles:

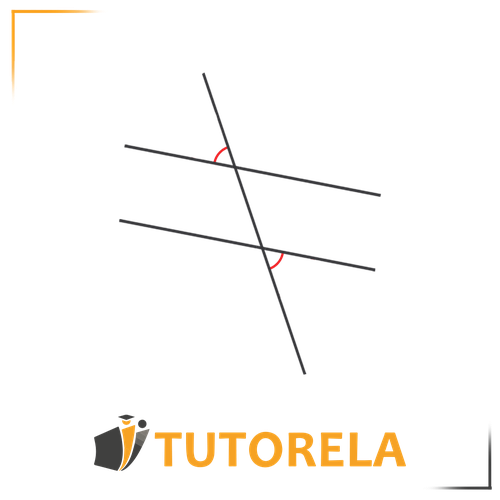
Note that in this illustration as well, you can observe that the two alternate angles are located in the internal part between the two parallel lines, and therefore they are alternate interior angles.

Bonus tip!
Alternate angles located in the external part outside the two parallel lines are called exterior alternate angles.

And now let's practice!
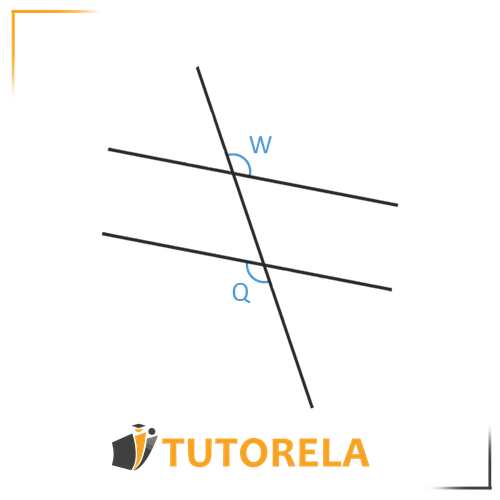
Here are two parallel lines and a line intersecting them.
a. Determine whether the angles shown are alternate angles.
b. Determine whether they are also alternate interior angles.

Solution:
a. Yes, the angles in the figure are alternate angles. They are not on the same side of the transversal and not on the same level relative to the line.
b. Yes, the alternate angles in the figure are interior since they are located in the inner part between the two parallel lines.

Another exercise:
Two parallel lines and a line intersecting them are shown.
a. Determine whether the angles shown are alternate angles
b. Determine whether they are alternate interior angles.

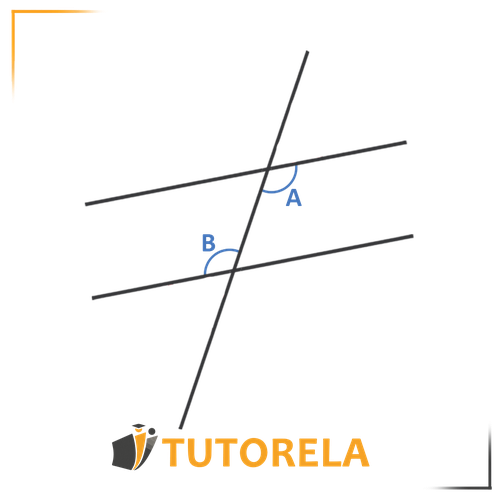
Solution:
a. Yes, the angles in the figure are alternate angles. They are not on the same level relative to the line and not on the same side of the transversal.
b. No. The angles are located in the external part outside the two parallel lines, therefore they are alternate angles but not interior ones.

Another exercise:
Here are two parallel lines and a line that intersects them.
Find the size of angle $A$
and determine whether angle $A$ and angle $B$ are alternate interior angles.
Given that: $B=100$

Solution:
According to the given information as well as the provided figue , we can determine that angle $A$ and angle $B$ are alternate angles. They are located between two parallel lines, each on a different side of the transversal and not on the same level relative to the line.
Alternate angles are equal to each other, therefore if $B=100$ we can conclude that angle $A=100$

Additionally, we can also determine that the two angles are alternate interior angles because they are both located in the interior part between the two parallel lines.

Additional Exercise:

In all drawings, the two lines are parallel to each other.
a. Determine whether there are alternate interior angles in both drawings.
b. If in drawing $1$ the marked angle $Q$ equals $130$, what is angle $W$?
c. Determine true or false - only alternate exterior angles are equal to each other.

1.

2.

Solution:
a. No, only in the second drawing the two angles are alternate interior angles given that they are located in the inner part of the lines.
In the first drawing, the two angles are alternate exterior angles since they are located in the outer part of the lines.

b. The two angles marked in the drawing $1$ are alternate angles and therefore they are equal.
From this we can conclude that angle $W$ is also equal to $130$.

C. Incorrect – exterior alternate angles are also equal to each other.